练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．设向量$\overrightarrow{a}$=（1，x），$\overrightarrow{b}$=（-2，2-x），若$\overrightarrow{a}$∥$\overrightarrow{b}$，则x=-2．

    分析 根据$\overrightarrow{a}∥\overrightarrow{b}$即可得到关于x的方程，解方程即可求出x的值．

    解答 解：∵$\overrightarrow{a}∥\overrightarrow{b}$；
    ∴1•（2-x）-（-2）•x=0；
    解得x=-2．
    故答案为：-2．

    点评 考查向量平行的概念，平行向量的坐标关系．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

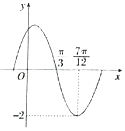    12．函数f（x）=Asin（ωx+φ）（A，ω，φ是常数，A＞0，ω＞0）的部分图象如图所示，则下列结论：①将f（x）的图象向左平移$\frac{π}{6}$个单位，所得到的函数是偶函数：②f（0）=1；③最小正周期为π；④$f（\frac{12π}{11}）＜f（\frac{14π}{13}）$；⑤$f（x）=-f（\frac{5π}{3}-x）$．其中正确的结论有（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．一半径为4m的水轮（如图），水轮圆心O距离水面2m，已知水轮每分钟转动4圈，如果当水轮上点P从水中浮现时（图中点P0）开始计时．
    （1）将点P距离水面的高度h（m）表示为时间t（s）的函数；
    （2）在水轮转动的一圈内，有多长时间点P距水面的高度超过4m．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．设a＞0，b＞0，且a+b=$\frac{1}{a}$+$\frac{1}{b}$．证明：
    （1）设$M=\frac{1}{a+1}+\frac{1}{b+1}$，$N=\frac{a}{a+1}+\frac{b}{b+1}$，求证M=N
    （2）a2+a＜2与b2+b＜2不可能同时成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．在区间（0，2）内随机取出两个数x，y，则1，x，y能作为三角形三条边的概率为（　　）
    A．$\frac{1}{8}$B．$\frac{3}{8}$C．$\frac{5}{8}$D．$\frac{7}{8}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．如图，四棱锥P-ABCD，底面ABCD是边长为2的菱形，$∠ABC=\frac{π}{3}$，且PA⊥平面ABCD．
    （Ⅰ）证明：平面PAC⊥平面PBD；
    （Ⅱ）设点E是线段AP的中点，且AE=1，求点E到平面PCD的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．求下列函数的导数：
    （1）y=（1-$\sqrt{x}$）（1+$\frac{1}{\sqrt{x}}$）
     （2）y=$\frac{lnx}{x}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．在区间（0，2）内随机取出两个数x，y，则1，x2，y能作为三角形三条边的概率为（　　）
    A．$\frac{{\sqrt{3}+1}}{4}$B．$\frac{{\sqrt{3}-1}}{2}$C．$\frac{{3-\sqrt{3}}}{4}$D．$\frac{{3-\sqrt{3}}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知函数f（x）=|x+a|+|x-2|．
    （1）若f（x）的最小值为4，求实数a的值；
    （2）若-1≤x≤0时，不等式f（x）≤|x-3|恒成立，求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案