
【题目】在正三棱柱![]() 中,
中,![]() ,点D是BC的中点,点
,点D是BC的中点,点![]() 在
在![]() 上,且
上,且![]() .
.

(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)求证:平面![]() ⊥平面
⊥平面![]() .
.
【答案】(1)详见解析 (2)详见解析
【解析】
试题分析:(1)证明线面平行,一般利用线面平行的判定定理,即从线线平行出发给予证明,而线线平行的寻找与论证往往需要利用平面几何知识,如本题利用三角形中位线性质得到线线平行.设![]() , 则
, 则![]() 是
是![]() 的中点,而已知
的中点,而已知![]() 是
是![]() 的中点,因此
的中点,因此![]() . (2)证明面面垂直,一般利用面面垂直的判定定理,即从线面垂直出发给予证明,而线面垂直的证明,往往需要多次利用线面垂直的性质定理与判定定理.由直三棱柱性质得侧棱垂直于底面,因此
. (2)证明面面垂直,一般利用面面垂直的判定定理,即从线面垂直出发给予证明,而线面垂直的证明,往往需要多次利用线面垂直的性质定理与判定定理.由直三棱柱性质得侧棱垂直于底面,因此![]() ,由正三角形性质得
,由正三角形性质得![]() ,因此
,因此![]() 平面
平面![]() .从而
.从而![]() . 又由平几何知识可得
. 又由平几何知识可得![]() ,因此
,因此![]() 平面
平面![]() .进而有平面
.进而有平面![]() ⊥平面
⊥平面![]() .
.
试题解析:(1) 记![]() ,连接
,连接![]() .
.![]()
∵四边形![]() 为矩形,∴
为矩形,∴![]() 是
是![]() 的中点,
的中点,
又∵![]() 是
是![]() 的中点,∴
的中点,∴![]() .·······3分
.·······3分
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ∥平面
∥平面![]() .·······6分
.·······6分

(2)∵![]() 是正三角形,
是正三角形,![]() 是
是![]() 的中点,
的中点,
∴![]() .
.
∵平面![]() ⊥平面
⊥平面![]() ,
,
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .·······9分
.·······9分
【或利用![]() ⊥平面
⊥平面![]() ,证明
,证明![]() 平面
平面![]() .】
.】
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() ,
,![]() ,
,![]() 是
是![]() 中点,
中点,
∴![]() ,
,
∴![]() ,·······10分
,·······10分
∴![]() ,∴
,∴![]() ,
,
∴![]() ,又
,又![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .·······12分
.·······12分
又∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .·······14分
.·······14分


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
【题目】200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,则时速在[50,70)的汽车大约( ) 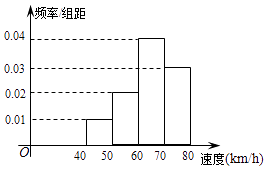
A.60辆
B.80辆
C.100辆
D.120辆
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]()
![]() 满足
满足![]() ,且
,且![]() ,正项数列
,正项数列![]() 满足
满足![]() ,其前7项和为42.
,其前7项和为42.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意正整数
,若对任意正整数![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)将数列![]() 的项按照“当
的项按照“当![]() 为奇数时,
为奇数时,![]() 放在前面;当
放在前面;当![]() 为偶数时,
为偶数时,![]() 放在前面”的要求进行排列,得到一个新的数列:
放在前面”的要求进行排列,得到一个新的数列:![]() ,求这个新数列的前
,求这个新数列的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点![]() 且离心率为
且离心率为![]() 的椭圆
的椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上.
轴上.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆的左准线与
是椭圆的左准线与![]() 轴的交点,过点
轴的交点,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,记椭圆
两点,记椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,上下两个顶点分别为
,上下两个顶点分别为![]() .当线段
.当线段![]() 的中点落在四边形
的中点落在四边形![]() 内(包括边界)时,求直线
内(包括边界)时,求直线![]() 斜率的取值范围.
斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
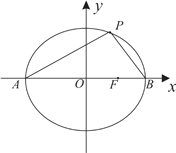
【题目】如图,已知椭圆![]() 的左右顶点分别为
的左右顶点分别为![]() ,右焦点为
,右焦点为![]() ,焦距为
,焦距为![]() ,点
,点![]() 是椭圆C上异于
是椭圆C上异于![]() 两点的动点,
两点的动点, ![]() 的面积最大值为
的面积最大值为![]() .
.
(1)求椭圆C的方程;
(2)若直线![]() 与直线
与直线![]() 交于点
交于点![]() ,试判断以
,试判断以![]() 为直径的圆与直线
为直径的圆与直线![]() 的位置关系,并作出证明.
的位置关系,并作出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 中,
中, ![]() 为正三角形,
为正三角形, ![]() ,
, ![]() ,
, ![]() 与
与![]() 中心
中心![]() 点,将
点,将![]() 沿边
沿边![]() 折起,使
折起,使![]() 点至
点至![]() 点,已知
点,已知![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
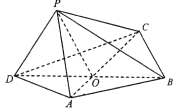
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求已知二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.某生产企业积极响应号召,大力研发新产品.为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]() ,如下表所示:
,如下表所示:

已知![]() .
.
(1)求出![]() 的值;
的值;
(2)已知变量![]() ,
, ![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (件)关于试销单价
(件)关于试销单价![]() (元)的线性回归方程
(元)的线性回归方程![]() ;
;
(3)用![]() 表示用正确的线性回归方程得到的与
表示用正确的线性回归方程得到的与![]() 对应的产品销量的估计值.当销售数据
对应的产品销量的估计值.当销售数据![]() 的残差的绝对值
的残差的绝对值![]() 时,则将销售数据
时,则将销售数据![]() 称为一个“好数据”.现从6个销售数据中任取2个,求抽取的2个销售数据中至少有1个是“好数据”的概率.
称为一个“好数据”.现从6个销售数据中任取2个,求抽取的2个销售数据中至少有1个是“好数据”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com