
 的值域;
的值域; 的单调区间.
的单调区间.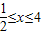 及对数函数的单调性可求函数的值域
及对数函数的单调性可求函数的值域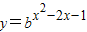 =
= ,结合二次函数与对数函数的单调性及复合函数的单调性可求函数的单调区间
,结合二次函数与对数函数的单调性及复合函数的单调性可求函数的单调区间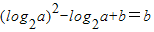
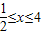
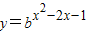 =
=
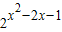 的单调减区间:(-∞,1);增区间:(1,+∞)
的单调减区间:(-∞,1);增区间:(1,+∞)

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| x |
| x2-x+1 |
查看答案和解析>>
科目:高中数学 来源:郑州二模 题型:解答题
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2013年高考数学压轴大题训练:函数与不等式的恒成立问题(解析版) 题型:解答题
 ,函数f(x)=x2,h(x)=2e lnx(e为自然常数).
,函数f(x)=x2,h(x)=2e lnx(e为自然常数).查看答案和解析>>
科目:高中数学 来源:2011年河南省郑州市高考数学二模试卷(理科)(解析版) 题型:解答题
 ,函数f(x)=x2,h(x)=2e lnx(e为自然常数).
,函数f(x)=x2,h(x)=2e lnx(e为自然常数).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com