【题目】已知向量 
=（3，﹣1）， 
=（2，1） 求：
（1）| 
|.
（2）求x的值使x +3 与3 ﹣2 为平行向量．
【答案】
（1）解：根据题意，向量 
=（3，﹣1）， 
=（2，1）
则 + =（5，0），
| + |= 
=5，
（2）解：向量 =（3，﹣1）， =（2，1）
则x +3 =（3x+6，3﹣x），3 ﹣2 =（5，﹣5），
若x +3 与3 ﹣2 为平行向量，
则有（3x+6）×（﹣5）=（3﹣x）×5，
解可得x=﹣ 
，
即当x=﹣ 时，向量x +3 与3 ﹣2 为平行向量．
【解析】（1）根据题意，由 、 的坐标可得向量 + 的坐标，由向量模的公式计算可得答案；（2）由 、 的坐标可得向量x +3 与3 ﹣2 的坐标，再结合向量平行的坐标表示公式可得（3x+6）×（﹣5）=（3﹣x）×5，解可得x的值，即可得答案．
【考点精析】认真审题，首先需要了解平面向量的坐标运算(坐标运算：设
，
则
;
;设
，则
)．
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】平面直角坐标系
中，椭圆
： 
（
）的离心率是
，抛物线
： 
的焦点
是
的一个顶点．
（1）求椭圆
的方程；
（2）设
是
上动点，且位于第一象限， 
在点
处的切线
与
交于不同的两点
， 
，线段
的中点为
，直线
与过
且垂直于
轴的直线交于点
．
（i）求证：点
在定直线上；
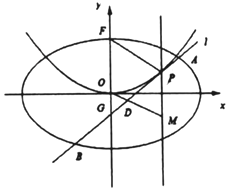
（ii）直线
与
轴交于点
，记
的面积为
， 
的面积为
，求
的最大值及取得最大值时点
的坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图为一简单组合体，其底面 ABCD为正方形，PD⊥平面ABCD，EC∥PD，且PD=AD=2EC=2． 
（1）求证：BE∥平面PDA；
（2）求四棱锥B﹣CEPD的体积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数 
（1）若m=1，求函数f（x）的定义域．
（2）若函数f（x）的值域为R，求实数m的取值范围．
（3）若函数f（x）在区间 
上是增函数，求实数m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知向量 
与 
．
（Ⅰ）若 
在 
方向上的投影为 
，求λ的值；
（Ⅱ）命题P：向量 与 的夹角为锐角；
命题q： 
，其中向量 
， 
=（ 
）（λ，α∈R）．若“p或q”为真命题，“p且q”为假命题，求λ的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆C1的圆心在坐标原点O，且恰好与直线l1：x﹣2y+3 
=0相切，点A为圆上一动点，AM⊥x轴于点M，且动点N满足 
，设动点N的轨迹为曲线C．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若直线l与椭圆C相交于不同两点A，B，且满足 
（O为坐标原点），求线段AB长度的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】交警随机抽取了途径某服务站的40辆小型轿车在经过某区间路段的车速（单位： 
），现将其分成六组为
后得到如图所示的频率分布直方图.
（1）某小型轿车途经该路段，其速度在
以上的概率是多少？
（2）若对车速在
两组内进一步抽测两辆小型轿车，求至少有一辆小型轿车速度在
内的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，设命题p：椭圆C： 
+ 
=1的焦点在x轴上；命题q：直线l：x﹣y+m=0与圆O：x2+y2=9有公共点． 若命题p、命题q中有且只有一个为真命题，求实数m的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
