
ЁОЬтФПЁПФГаЃЮЊСЫМЭФюЁАжаЙњКьОќГЄеї90жмФъЁБЃЌдіЧПбЇЩњЖдЁАГЄеїОЋЩёЁБЕФЩюПЬРэНтЃЌдкШЋаЃзщжЏСЫвЛДЮгаЙиЁАГЄеїЁБЕФжЊЪЖОКШќЃЌОЙ§ГѕШќЁЂИДШќЃЌМзЁЂввСНИіДњБэЖг(УПЖг3ШЫ)НјШыСЫОіШќЃЌЙцЖЈУПШЫЛиД№вЛИіЮЪЬтЃЌД№ЖдЮЊБОЖггЎЕУ20ЗжЃЌД№ДэЕУ0Зж.МйЩшМзЖгжаУПШЫД№ЖдЕФИХТЪОљЮЊ ![]() ЃЌввЖгжа3ШЫД№ЖдЕФИХТЪЗжБ№ЮЊ
ЃЌввЖгжа3ШЫД№ЖдЕФИХТЪЗжБ№ЮЊ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌЧвИїШЫЛиД№е§ШЗгыЗёЯрЛЅжЎМфУЛгагАЯьЃЌгУ
ЃЌЧвИїШЫЛиД№е§ШЗгыЗёЯрЛЅжЎМфУЛгагАЯьЃЌгУ ![]() БэЪОввЖгЕФзмЕУЗж.
БэЪОввЖгЕФзмЕУЗж.
ЃЈ1ЃЉЧѓ ![]() ЕФЗжВМСаКЭОљжЕЃЛ
ЕФЗжВМСаКЭОљжЕЃЛ
ЃЈ2ЃЉЧѓМзЁЂввСНЖгзмЕУЗжжЎКЭЕШгк40ЗжЧвМзЖгЛёЪЄЕФИХТЪ.
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКгЩЬтвтжЊЃЌ ![]() ЕФЫљгаПЩФмШЁжЕЮЊ0ЃЌ20ЃЌ40ЃЌ60.
ЕФЫљгаПЩФмШЁжЕЮЊ0ЃЌ20ЃЌ40ЃЌ60.
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() .
.
![]() ЕФЗжВМСаЮЊЃК
ЕФЗжВМСаЮЊЃК
| 0 | 20 | 40 | 60 |
|
|
|
|
|
Ыљвд ![]() .
.
ЃЈ2ЃЉНтЃКМЧЁАМзЖгЕУ40ЗжЃЌввЖгЕУ0ЗжЁБЮЊЪТМў ![]() .
.
гж ![]() ЃЌ
ЃЌ
ЙЪМзЁЂввСНЖгзмЕУЗжжЎКЭЮЊ40ЗжЧвМзЖгЛёЪЄЕФИХТЪЮЊЃК ![]() .
.
ЁОНтЮіЁПЃЈ1ЃЉУїШЗ ![]() ЕФЫљгаПЩФмШЁжЕЃЌВЂШЗЖЈЯргІЕФИХТЪЃЌДгЖјЕУЕНЗжВМСаМАЦкЭћЃЛЃЈ2ЃЉМЧЁАМзЖгЕУ40ЗжЃЌввЖгЕУ0ЗжЁБЮЊЪТМў
ЕФЫљгаПЩФмШЁжЕЃЌВЂШЗЖЈЯргІЕФИХТЪЃЌДгЖјЕУЕНЗжВМСаМАЦкЭћЃЛЃЈ2ЃЉМЧЁАМзЖгЕУ40ЗжЃЌввЖгЕУ0ЗжЁБЮЊЪТМў ![]() ЃЌдђ
ЃЌдђ ![]() ЁЃ
ЁЃ
ЁОПМЕуОЋЮіЁПЙигкБОЬтПМВщЕФРыЩЂаЭЫцЛњБфСПМАЦфЗжВМСаЃЌашвЊСЫНтдкЩфЛїЁЂВњЦЗМьбщЕШР§згжаЃЌЖдгкЫцЛњБфСПXПЩФмШЁЕФжЕЃЌЮвУЧПЩвдАДвЛЖЈДЮађвЛвЛСаГіЃЌетбљЕФЫцЛњБфСПНазіРыЩЂаЭЫцЛњБфСПЃЎРыЩЂаЭЫцЛњБфСПЕФЗжВМСаЃКвЛАуЕФ,ЩшРыЩЂаЭЫцЛњБфСПXПЩФмШЁЕФжЕЮЊx1,x2,.....,xi,......,xnЃЌXШЁУПвЛИіжЕ xi(i=1,2,......ЃЉЕФИХТЪP(ІЮ=xiЃЉЃНPiЃЌдђГЦБэЮЊРыЩЂаЭЫцЛњБфСПX ЕФИХТЪЗжВМЃЌМђГЦЗжВМСаВХФмЕУГіе§ШЗД№АИЃЎ


 вЛОэИуЖЈЯЕСаД№АИ
вЛОэИуЖЈЯЕСаД№АИ УћаЃзївЕБОЯЕСаД№АИ
УћаЃзївЕБОЯЕСаД№АИ ЧсЧЩЖсЙкжмВтдТПМжБЭЈУћаЃЯЕСаД№АИ
ЧсЧЩЖсЙкжмВтдТПМжБЭЈУћаЃЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЕФвЛИіФкНЧЮЊ
ЕФвЛИіФкНЧЮЊ![]() ЃЌВЂЧвШ§БпГЄЙЙГЩЙЋВюЮЊ4ЕФЕШВюЪ§Са,дђ
ЃЌВЂЧвШ§БпГЄЙЙГЩЙЋВюЮЊ4ЕФЕШВюЪ§Са,дђ![]() ЕФУцЛ§ЮЊЃЈ ЃЉ
ЕФУцЛ§ЮЊЃЈ ЃЉ
A. 15 B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉСНИіЙВщюИДЪ§ЕФВюЪЧДПащЪ§ЃЛЃЈ2ЃЉСНИіЙВщюИДЪ§ЕФКЭВЛвЛЖЈЪЧЪЕЪ§ЃЛЃЈ3ЃЉШєИДЪ§a+biЃЈaЃЌbЁЪRЃЉЪЧФГвЛдЊЖўДЮЗНГЬЕФИљЃЌдђaЉbiЪЧвВвЛЖЈЪЧетИіЗНГЬЕФИљЃЛЃЈ4ЃЉШєzЮЊащЪ§ЃЌдђzЕФЦНЗНИљЮЊащЪ§ЃЌ
Цфжае§ШЗЕФИіЪ§ЮЊЃЈ ЃЉ
A.3
B.2
C.1
D.0
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fnЃЈxЃЉ= ![]() x3Љ
x3Љ ![]() ЃЈn+1ЃЉx2+xЃЈnЁЪN*ЃЉЃЌЪ§Са{an}Тњзуan+1=f'nЃЈanЃЉЃЌa1=3ЃЎ
ЃЈn+1ЃЉx2+xЃЈnЁЪN*ЃЉЃЌЪ§Са{an}Тњзуan+1=f'nЃЈanЃЉЃЌa1=3ЃЎ
ЃЈ1ЃЉЧѓa2 ЃЌ a3 ЃЌ a4ЃЛ
ЃЈ2ЃЉИљОнЃЈ1ЃЉВТЯыЪ§Са{an}ЕФЭЈЯюЙЋЪНЃЌВЂгУЪ§бЇЙщФЩЗЈжЄУїЃЛ
ЃЈ3ЃЉЧѓжЄЃК ![]() +
+ ![]() +Ё+
+Ё+ ![]() ЃМ
ЃМ ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са![]() жаЃЌ
жаЃЌ![]() ЃЎ
ЃЎ
(1)ЧѓжЄЃКЪ§Са![]() ЪЧЕШБШЪ§СаЃЛ
ЪЧЕШБШЪ§СаЃЛ
(2)ЧѓЪ§Са![]() ЕФЭЈЯюЙЋЪНЃЛ
ЕФЭЈЯюЙЋЪНЃЛ
(3)Щш![]() ЃЌШєЖдШЮвт
ЃЌШєЖдШЮвт![]() ЃЌга
ЃЌга![]() КуГЩСЂЃЌЧѓЪЕЪ§
КуГЩСЂЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ ![]() ЕФРыаФТЪЮЊ
ЕФРыаФТЪЮЊ ![]() ЃЌЦфжазѓНЙЕуЮЊ
ЃЌЦфжазѓНЙЕуЮЊ ![]() .
.
ЃЈ1ЃЉЧѓЭждВ ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉЙ§ ![]() ЕФжБЯп
ЕФжБЯп ![]() гыЭждВ
гыЭждВ ![]() ЯрНЛгк
ЯрНЛгк ![]() СНЕуЃЌШє
СНЕуЃЌШє ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ ![]() ЃЌЧѓвд
ЃЌЧѓвд ![]() ЮЊдВаФЧвгыжБЯп
ЮЊдВаФЧвгыжБЯп ![]() ЯрЧаЕФдВЕФЗНГЬ.
ЯрЧаЕФдВЕФЗНГЬ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌгЮПЭДгФГТУгЮОАЧјЕФОАЕу![]() ДІЯТЩЯжС
ДІЯТЩЯжС![]() ДІгаСНжжТЗОЖЃЎвЛжжЪЧДг
ДІгаСНжжТЗОЖЃЎвЛжжЪЧДг![]() бижБЯпВНааЕН
бижБЯпВНааЕН![]() ЃЌСэвЛжжЪЧЯШДг
ЃЌСэвЛжжЪЧЯШДг![]() биЫїЕРГЫРТГЕЕН
биЫїЕРГЫРТГЕЕН![]() ЃЌШЛКѓДг
ЃЌШЛКѓДг![]() бижБЯпВНааЕН
бижБЯпВНааЕН![]() ЃЎЯжгаМзЁЂввСНЮЛгЮПЭДг
ЃЎЯжгаМзЁЂввСНЮЛгЮПЭДг![]() ДІЯТЩНЃЌМзби
ДІЯТЩНЃЌМзби![]() дШЫйВНааЃЌЫйЖШЮЊ
дШЫйВНааЃЌЫйЖШЮЊ![]() ЃЎдкМзГіЗЂ
ЃЎдкМзГіЗЂ![]() КѓЃЌввДг
КѓЃЌввДг![]() ГЫРТГЕЕН
ГЫРТГЕЕН![]() ЃЌдк
ЃЌдк![]() ДІЭЃСє
ДІЭЃСє![]() КѓЃЌдйДг
КѓЃЌдйДг![]() дШЫйВНааЕН
дШЫйВНааЕН![]() ЃЌМйЩшРТГЕдШЫйжБЯпдЫЖЏЕФЫйЖШЮЊ
ЃЌМйЩшРТГЕдШЫйжБЯпдЫЖЏЕФЫйЖШЮЊ![]() ЃЌЩНТЗ
ЃЌЩНТЗ![]() ГЄЮЊ1260
ГЄЮЊ1260![]() ЃЌОВтСП
ЃЌОВтСП![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
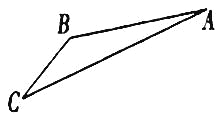
ЃЈ1ЃЉЧѓЫїЕР![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ2ЃЉЮЪЃКввГіЗЂЖрЩй![]() КѓЃЌввдкРТГЕЩЯгыМзЕФОрРызюЖЬЃП
КѓЃЌввдкРТГЕЩЯгыМзЕФОрРызюЖЬЃП
ЃЈ3ЃЉЮЊЪЙСНЮЛгЮПЭдк![]() ДІЛЅЯрЕШД§ЕФЪБМфВЛГЌЙ§
ДІЛЅЯрЕШД§ЕФЪБМфВЛГЌЙ§![]() ЃЌввВНааЕФЫйЖШгІПижЦдкЪВУДЗЖЮЇФкЃП
ЃЌввВНааЕФЫйЖШгІПижЦдкЪВУДЗЖЮЇФкЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫЋЧњЯп ![]() =1ЃЈaЃО1ЃЌbЃО0ЃЉЕФНЙЕуОрЮЊ2cЃЌжБЯпlЙ§ЕуЃЈaЃЌ0ЃЉКЭЃЈ0ЃЌbЃЉЃЌЧвЕуЃЈ1ЃЌ0ЃЉЕНжБЯпlЕФОрРыгыЕуЃЈЉ1ЃЌ0ЃЉЕНжБЯпlЕФОрРыжЎКЭ
=1ЃЈaЃО1ЃЌbЃО0ЃЉЕФНЙЕуОрЮЊ2cЃЌжБЯпlЙ§ЕуЃЈaЃЌ0ЃЉКЭЃЈ0ЃЌbЃЉЃЌЧвЕуЃЈ1ЃЌ0ЃЉЕНжБЯпlЕФОрРыгыЕуЃЈЉ1ЃЌ0ЃЉЕНжБЯпlЕФОрРыжЎКЭ ![]() ЃЎЧѓЫЋЧњЯпЕФРыаФТЪeЕФШЁжЕЗЖЮЇЃЎ
ЃЎЧѓЫЋЧњЯпЕФРыаФТЪeЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са{an}ЕФЧАnЯюКЭЮЊSn ЃЌ Тњзуan= ![]() +2nЉ2ЃЌnЁЪN* ЃЌ ЧвS2=6ЃЎ
+2nЉ2ЃЌnЁЪN* ЃЌ ЧвS2=6ЃЎ
ЃЈ1ЃЉЧѓЪ§Са{an}ЕФЭЈЯюЙЋЪНЃЛ
ЃЈ2ЃЉжЄУїЃК ![]() +
+ ![]() +
+ ![]() +Ё+
+Ё+ ![]() ЃМ
ЃМ ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com