
°ĺŐ‚ńŅ°Ņ ‹ÕĽ»Á∆šņīĶń–¬Ļŕ“Ŗ«ťĶń”įŌž£¨»ęĻķłųĶō—ß–£∂ľÕ∆≥Ŕ2020ńÍĶńīļľĺŅ™—ß.ń≥—ß–£°įÕ£Ņő≤ĽÕ£—ß°Ī£¨ņŻ”√‘∆Ņő∆ĹŐ®ŐŠĻ©√‚∑—ŌŖ…ŌŅő≥Ő.ł√—ß–£ő™ŃňĹ‚—ß…ķ∂‘ŌŖ…ŌŅő≥ŐĶń¬ķ“‚≥Ő∂»£¨ňśĽķ≥ť»°Ńň500√Ż—ß…ķ∂‘ł√ŌŖ…ŌŅő≥Ő∆ņ∑÷.∆š∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ»ÁŌ¬£ļ»Űłýĺ›∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľĶ√ĶĹĶń∆ņ∑÷ĶÕ”ŕ80∑÷ĶńłŇ¬ Ļņľ∆÷Ķő™0.45.
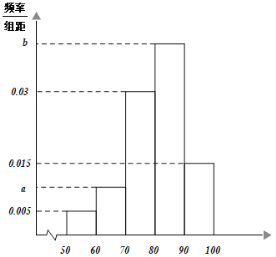
£®1£©£®i£©«ů÷Ī∑ĹÕľ÷–Ķńa£¨b÷Ķ£Ľ
£®ii£©»Ű∆ņ∑÷Ķń∆Ĺĺý÷ĶļÕ÷ŕ żĺý≤ĽĶÕ”ŕ80∑÷ ”ő™¬ķ“‚£¨Ň–∂Ōł√–£—ß…ķ∂‘ŌŖ…ŌŅő≥Ő «∑٬ķ“‚£Ņ≤ĘňĶ√ųņŪ”…£®Õ¨“Ľ◊ť÷–Ķń żĺ›”√ł√◊ť«ÝľšĶń÷–Ķ„÷Ķő™īķĪŪ£©£Ľ
£®2£©»Ű≤…”√∑÷≤„≥ť—ýĶń∑Ĺ∑®£¨ī”—ýĪĺ∆ņ∑÷‘ŕ[60£¨70£©ļÕ[90£¨100]ńŕĶń—ß…ķ÷–Ļ≤≥ť»°5»ňĹÝ––≤‚ ‘ņīľž—ťňŻ√«ĶńÕÝŅő—ßŌį–ßĻŻ£¨‘Ŕī”÷–—°»°2»ňĹÝ––łķ◊Ŕ∑÷őŲ£¨«ů’‚2»ň÷–÷Ń…Ŕ“Ľ»ň∆ņ∑÷‘ŕ[60£¨70£©ńŕĶńłŇ¬ .
°ĺīūįł°Ņ£®1£©£®i£©a£Ĺ0.01£Ľb£Ĺ0.04£®ii£©ł√–£—ß…ķ∂‘ŌŖ…ŌŅő≥Ő¬ķ“‚£¨ŌÍľŻĹ‚őŲ£®2£©![]()
°ĺĹ‚őŲ°Ņ
£®1£©![]() ”…∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ÷––°ĺō–ő√śĽż÷ģļÕő™1£¨ń‹«ů≥Ų
”…∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ÷––°ĺō–ő√śĽż÷ģļÕő™1£¨ń‹«ů≥Ų![]() £¨
£¨![]() £ģ
£ģ
![]() ”…∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľń‹«ů≥Ų∆ņ∑÷Ķń÷ŕ żļÕ∆ņ∑÷Ķń∆Ĺĺý÷Ķ£¨ī”∂ÝĶ√ĶĹł√–£—ß…ķ∂‘ŌŖ…ŌŅő≥Ő¬ķ“‚£ģ
”…∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľń‹«ů≥Ų∆ņ∑÷Ķń÷ŕ żļÕ∆ņ∑÷Ķń∆Ĺĺý÷Ķ£¨ī”∂ÝĶ√ĶĹł√–£—ß…ķ∂‘ŌŖ…ŌŅő≥Ő¬ķ“‚£ģ
£®2£©”…Ő‚÷™∆ņ∑÷‘ŕ![]() £¨
£¨![]() ļÕ
ļÕ![]() £¨
£¨![]() ńŕĶń∆Ķ¬ ∑÷Īūő™0.1ļÕ0.15£¨‘Ú≥ť»°Ķń5»ň÷–£¨∆ņ∑÷‘ŕ
ńŕĶń∆Ķ¬ ∑÷Īūő™0.1ļÕ0.15£¨‘Ú≥ť»°Ķń5»ň÷–£¨∆ņ∑÷‘ŕ![]() £¨
£¨![]() ńŕĶńő™2»ň£¨∆ņ∑÷‘ŕ
ńŕĶńő™2»ň£¨∆ņ∑÷‘ŕ![]() £¨
£¨![]() Ķń”–3»ň£¨ľ«∆ņ∑÷‘ŕ
Ķń”–3»ň£¨ľ«∆ņ∑÷‘ŕ![]() £¨
£¨![]() ńŕĶń3őĽ—ß…ķő™
ńŕĶń3őĽ—ß…ķő™![]() £¨
£¨![]() £¨
£¨![]() £¨∆ņ∑÷‘ŕ
£¨∆ņ∑÷‘ŕ![]() £¨
£¨![]() ńŕĶń2őĽ—ß…ķ’‚
ńŕĶń2őĽ—ß…ķ’‚![]() £¨
£¨![]() £¨ī”5»ň÷–»ő—°2»ň£¨ņŻ”√Ń–ĺŔ∑®ń‹«ů≥Ų’‚2»ň÷–÷Ń…Ŕ“Ľ»ň∆ņ∑÷‘ŕ
£¨ī”5»ň÷–»ő—°2»ň£¨ņŻ”√Ń–ĺŔ∑®ń‹«ů≥Ų’‚2»ň÷–÷Ń…Ŕ“Ľ»ň∆ņ∑÷‘ŕ![]() £¨
£¨![]() ĶńłŇ¬ £ģ
ĶńłŇ¬ £ģ
Ĺ‚£ļ£®1£©![]() ”…“—÷™Ķ√
”…“—÷™Ķ√![]() £¨
£¨
Ĺ‚Ķ√![]() £¨
£¨
”÷![]() £¨
£¨![]() £ģ
£ģ
![]() ”…∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľĶ√∆ņ∑÷Ķń÷ŕ żő™85£¨
”…∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľĶ√∆ņ∑÷Ķń÷ŕ żő™85£¨
∆ņ∑÷Ķń∆Ĺĺý÷Ķő™![]() £¨
£¨
![]() ł√–£—ß…ķ∂‘ŌŖ…ŌŅő≥Ő¬ķ“‚£ģ
ł√–£—ß…ķ∂‘ŌŖ…ŌŅő≥Ő¬ķ“‚£ģ
£®2£©”…Ő‚÷™∆ņ∑÷‘ŕ![]() £¨
£¨![]() ļÕ
ļÕ![]() £¨
£¨![]() ńŕĶń∆Ķ¬ ∑÷Īūő™0.1ļÕ0.15£¨
ńŕĶń∆Ķ¬ ∑÷Īūő™0.1ļÕ0.15£¨
‘Ú≥ť»°Ķń5»ň÷–£¨∆ņ∑÷‘ŕ![]() £¨
£¨![]() ńŕĶńő™2»ň£¨∆ņ∑÷‘ŕ
ńŕĶńő™2»ň£¨∆ņ∑÷‘ŕ![]() £¨
£¨![]() Ķń”–3»ň£¨
Ķń”–3»ň£¨
ľ«∆ņ∑÷‘ŕ![]() £¨
£¨![]() ńŕĶń3őĽ—ß…ķő™
ńŕĶń3őĽ—ß…ķő™![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
∆ņ∑÷‘ŕ![]() £¨
£¨![]() ńŕĶń2őĽ—ß…ķ’‚
ńŕĶń2őĽ—ß…ķ’‚![]() £¨
£¨![]() £¨
£¨
‘Úī”5»ň÷–»ő—°2»ňĶńňý”–Ņ…ń‹ĹŠĻŻő™£ļ
![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨Ļ≤10÷÷£¨
£¨Ļ≤10÷÷£¨
∆š÷–£¨∆ņ∑÷‘ŕ![]() £¨
£¨![]() ńŕĶńŅ…ń‹ĹŠĻŻő™
ńŕĶńŅ…ń‹ĹŠĻŻő™![]() £¨
£¨![]() £¨
£¨![]() £¨Ļ≤3÷÷£¨
£¨Ļ≤3÷÷£¨
![]() ’‚2»ň÷–÷Ń…Ŕ“Ľ»ň∆ņ∑÷‘ŕ
’‚2»ň÷–÷Ń…Ŕ“Ľ»ň∆ņ∑÷‘ŕ![]() £¨
£¨![]() ĶńłŇ¬ ő™
ĶńłŇ¬ ő™![]() £ģ
£ģ


 Ľ™∂ę ¶īůįś“ĽŅő“ĽŃ∑ŌĶŃ–īūįł
Ľ™∂ę ¶īůįś“ĽŅő“ĽŃ∑ŌĶŃ–īūįł √ŌĹ®∆Ĺ√Ż–£ŅľĺŪŌĶŃ–īūįł
√ŌĹ®∆Ĺ√Ż–£ŅľĺŪŌĶŃ–īūįł
| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ļĮ żf£®x£©£Ĺxlnx£¨ļĮ żg£®x£©£Ĺkx©Ācosx‘ŕĶ„![]() ī¶Ķń«–ŌŖ∆Ĺ––”ŕx÷Š.
ī¶Ķń«–ŌŖ∆Ĺ––”ŕx÷Š.
£®1£©«ůļĮ żf£®x£©Ķńľę÷Ķ£Ľ
£®2£©Ő÷¬ŘļĮ żF£®x£©£Ĺg£®x£©©Āf£®x£©ĶńŃ„Ķ„ĶńłŲ ż.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™Õ÷‘≤![]()
![]() ĶńņŽ–ń¬ ő™
ĶńņŽ–ń¬ ő™![]() £¨ĹĻĺŗő™
£¨ĹĻĺŗő™![]() £¨÷ĪŌŖ
£¨÷ĪŌŖ![]() ĻżÕ÷‘≤Ķń
ĻżÕ÷‘≤Ķń![]() ◊ůĹĻĶ„.
◊ůĹĻĶ„.
£®1£©«ůÕ÷‘≤![]() ĶńĪÍ◊ľ∑Ĺ≥Ő£Ľ
ĶńĪÍ◊ľ∑Ĺ≥Ő£Ľ
£®2£©»Ű÷ĪŌŖ![]() ”Ž
”Ž![]() ÷ŠĹĽ”ŕĶ„
÷ŠĹĽ”ŕĶ„![]() «Õ÷‘≤
«Õ÷‘≤![]() …ŌĶńŃĹłŲ∂ĮĶ„,
…ŌĶńŃĹłŲ∂ĮĶ„,![]() Ķń∆Ĺ∑÷ŌŖ‘ŕ
Ķń∆Ĺ∑÷ŌŖ‘ŕ![]() ÷Š…Ō,
÷Š…Ō,![]() . ‘Ň–∂Ō÷ĪŌŖ
. ‘Ň–∂Ō÷ĪŌŖ![]() «∑ŮĻż∂®Ķ„£¨»ŰĻż∂®Ķ„£¨«ů≥Ų∂®Ķ„◊ÝĪÍ;»Ű≤ĽĻż∂®Ķ„£¨«ŽňĶ√ųņŪ”….
«∑ŮĻż∂®Ķ„£¨»ŰĻż∂®Ķ„£¨«ů≥Ų∂®Ķ„◊ÝĪÍ;»Ű≤ĽĻż∂®Ķ„£¨«ŽňĶ√ųņŪ”….
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ļĮ żf£®x£©![]() |2x©Ā3|£¨g£®x£©
|2x©Ā3|£¨g£®x£©![]() |2x+a+b|.
|2x+a+b|.
£®1£©Ĺ‚≤ĽĶ» Ĺf£®x£©![]() x2£Ľ
x2£Ľ
£®2£©ĶĪa![]() 0£¨b
0£¨b![]() 0 Ī£¨»ŰF£®x£©
0 Ī£¨»ŰF£®x£©![]() f£®x£©+g£®x£©Ķń÷Ķ”Úő™[5£¨+°ř£©£¨«ů÷§£ļ
f£®x£©+g£®x£©Ķń÷Ķ”Úő™[5£¨+°ř£©£¨«ů÷§£ļ![]() .
.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕňńņ‚◊∂![]() ÷–£¨
÷–£¨![]() «ĪŖ≥§ő™4Ķń’ż»żĹ«–ő£¨
«ĪŖ≥§ő™4Ķń’ż»żĹ«–ő£¨![]() «“
«“![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨Mő™AB÷–Ķ„£ģ
£¨Mő™AB÷–Ķ„£ģ
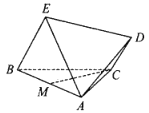
£®ĘŮ£©÷§√ų£ļ![]() ∆Ĺ√śADE£Ľ
∆Ĺ√śADE£Ľ
£®ĘÚ£©«ů÷ĪŌŖCA”Ž∆Ĺ√śBCDEňý≥…Ĺ«Ķń’żŌ“÷Ķ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ![]() ÷–£¨‘≤
÷–£¨‘≤![]() …Ō“ĽĶ„
…Ō“ĽĶ„![]() ī¶Ķń«–ŌŖ
ī¶Ķń«–ŌŖ![]() ∑÷ĪūĹĽ
∑÷ĪūĹĽ![]() ÷Š
÷Š![]() ÷Š”ŕĶ„
÷Š”ŕĶ„![]() £¨“‘
£¨“‘![]() ő™∂•Ķ„«““‘
ő™∂•Ķ„«““‘![]() ő™÷––ńĶńÕ÷‘≤ľ«◊ų
ő™÷––ńĶńÕ÷‘≤ľ«◊ų![]() £¨÷ĪŌŖ
£¨÷ĪŌŖ![]() ĹĽ
ĹĽ![]() ”ŕ
”ŕ![]() ŃĹĶ„.
ŃĹĶ„.
£®1£©»ŰÕ÷‘≤![]() ĶńņŽ–ń¬ ő™
ĶńņŽ–ń¬ ő™![]() £¨«ů
£¨«ů![]() Ķ„◊ÝĪÍ£Ľ
Ķ„◊ÝĪÍ£Ľ
£®2£©÷§√ų£ļňńĪŖ–ő![]() Ķń√śĽż
Ķń√śĽż![]() .
.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņī”ń≥Ķō«Ý–°—ßĶń∆ŕń©Ņľ ‘÷–≥ť»°≤Ņ∑÷—ß…ķĶń ż—ß≥…ľ®£¨”…≥ť≤ťĹŠĻŻĶ√ĶĹ»ÁÕľĶń∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ£¨∑÷ ż¬š‘ŕ«Ýľš![]() £¨
£¨![]() £¨
£¨![]() ńŕĶń∆Ķ¬ ÷ģĪ»ő™
ńŕĶń∆Ķ¬ ÷ģĪ»ő™![]() £ģ
£ģ
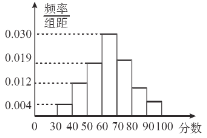
£®1£©«ů’‚–©—ß…ķĶń∑÷ ż¬š‘ŕ«Ýľš![]() ńŕĶń∆Ķ¬ £Ľ
ńŕĶń∆Ķ¬ £Ľ
£®2£©»ŰĹę∆Ķ¬ ”ő™łŇ¬ £¨ī”ł√Ķō«Ý–°—ßĶń’‚–©—ß…ķ÷–ňśĽķ≥ť»°3»ň£¨ľ«’‚3»ň÷–≥…ľ®őĽ”ŕ«Ýľš![]() ńŕĶń»ň żő™
ńŕĶń»ň żő™![]() £¨«ů
£¨«ů![]() Ķń∑÷≤ľŃ–”Ž ż—ß∆ŕÕŻ£ģ
Ķń∑÷≤ľŃ–”Ž ż—ß∆ŕÕŻ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»Ű żŃ–![]() ¬ķ◊„n°›2 Ī£¨
¬ķ◊„n°›2 Ī£¨![]() £¨‘Ú≥∆ żŃ–
£¨‘Ú≥∆ żŃ–![]() (n
(n![]() )ő™
)ő™![]() Ķń°įL żŃ–°Ī£ģ
Ķń°įL żŃ–°Ī£ģ
£®1£©»Ű![]() £¨«“
£¨«“![]() Ķń°įL żŃ–°Īő™
Ķń°įL żŃ–°Īő™![]() £¨«ů żŃ–
£¨«ů żŃ–![]() ĶńÕ®ŌÓĻę Ĺ£Ľ
ĶńÕ®ŌÓĻę Ĺ£Ľ
£®2£©»Ű![]() £¨«“
£¨«“![]() Ķń°įL żŃ–°Īő™Ķ›‘Ų żŃ–£¨«ůkĶń»°÷Ķ∑∂őߣĽ
Ķń°įL żŃ–°Īő™Ķ›‘Ų żŃ–£¨«ůkĶń»°÷Ķ∑∂őߣĽ
£®3£©»Ű![]() £¨∆š÷–p£ĺ1£¨ľ«
£¨∆š÷–p£ĺ1£¨ľ«![]() Ķń°įL żŃ–°ĪĶń«įnŌÓļÕő™
Ķń°įL żŃ–°ĪĶń«įnŌÓļÕő™![]() £¨ ‘Ň–∂Ō «∑Ůīś‘ŕĶ»≤Ó żŃ–
£¨ ‘Ň–∂Ō «∑Ůīś‘ŕĶ»≤Ó żŃ–![]() £¨∂‘»ő“‚n
£¨∂‘»ő“‚n![]() £¨∂ľ”–
£¨∂ľ”–![]() ≥…ŃĘ£¨≤Ę÷§√ųń„ĶńĹŠ¬Ř£ģ
≥…ŃĘ£¨≤Ę÷§√ųń„ĶńĹŠ¬Ř£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ‘ŕňńņ‚◊∂P-ABCD÷–£¨Ķ◊√śABCDő™÷ĪĹ«Ő›–ő£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨«“∆Ĺ√ś
£¨«“∆Ĺ√ś![]() ∆Ĺ√śABCD.
∆Ĺ√śABCD.
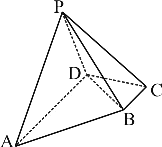
£®1£©«ů÷§£ļ![]() £Ľ
£Ľ
£®2£©‘ŕŌŖ∂őPA…Ō «∑Ůīś‘ŕ“ĽĶ„M£¨ Ļ∂Ģ√śĹ«M-BC-DĶńīů–°ő™![]() £Ņ»Űīś‘ŕ£¨«ů≥Ų
£Ņ»Űīś‘ŕ£¨«ů≥Ų![]() Ķń÷Ķ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”….
Ķń÷Ķ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”….
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com