
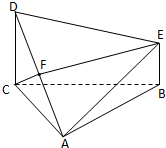
 已知D、E分别在平面ABC的同侧,且DC⊥平面ABC,EB⊥平面ABC,DC=2,△ABC是边长为2的正三角形,F是AD中点.
已知D、E分别在平面ABC的同侧,且DC⊥平面ABC,EB⊥平面ABC,DC=2,△ABC是边长为2的正三角形,F是AD中点. 解:(1)取AC中点G,连接FG、BG,则FG∥DC∥BE,
解:(1)取AC中点G,连接FG、BG,则FG∥DC∥BE,| 3 |
| BE |
| n |
| AD |
| 3 |
| DE |
|
|
| 3 |
| n |
| 3 |
| BE |
| n |
| ||||
|
|
| 2 | ||
2
|
| ||
| 2 |
| BE |
| n |


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| △ADE的面积 |
| A′H2 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年甘肃省兰州一中高二(下)期末数学试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2011年江苏省南通市启东中学高三数学考前辅导材料(1)(解析版) 题型:解答题
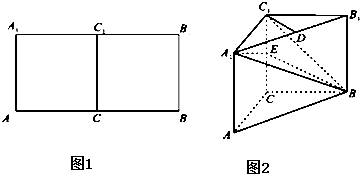
 的正△ABC,点D,E分别在边AB,AC上,且DE∥BC,以DE为折痕,把△ADE折起至△A'DE,使点A'在平面BCED上的射影H始终落在BC边上,记
的正△ABC,点D,E分别在边AB,AC上,且DE∥BC,以DE为折痕,把△ADE折起至△A'DE,使点A'在平面BCED上的射影H始终落在BC边上,记 ,则S的取值范围为 .
,则S的取值范围为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com