
 ,设AB=x米,BC=y米.
,设AB=x米,BC=y米.
 ,利用基本不等式,即可求得所用材料最少.
,利用基本不等式,即可求得所用材料最少. 解:(1)如图,等腰梯形CDEF中,DH是高,则EH=AB=x,DH=EH•tan∠FED=
解:(1)如图,等腰梯形CDEF中,DH是高,则EH=AB=x,DH=EH•tan∠FED=
 =6,
=6,
 >0,∴0<x<2
>0,∴0<x<2 (0<x<2)
(0<x<2) ,∴cos∠FED=
,∴cos∠FED= ,
,
 =
= ≥
≥
 ,即
,即 时取等号
时取等号 =
=
 米,BC=
米,BC= 米时,所用材料最少.
米时,所用材料最少.

科目:高中数学 来源: 题型:
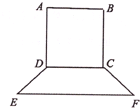 要制作一个如图的框架(单位:米),要求所围成的总面积为19.5(米2),其中ABCD是一个矩形,EFCD是一个等腰梯形,梯形高h=
要制作一个如图的框架(单位:米),要求所围成的总面积为19.5(米2),其中ABCD是一个矩形,EFCD是一个等腰梯形,梯形高h=| 1 |
| 2 |
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
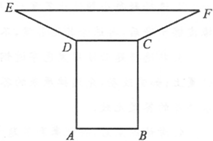 (2012•湛江二模)要制作一个如图的框架(单位:米),要求所围成的面积为6米2,其中ABCD是一个矩形,EFCD是一个等腰梯形,EF=3CD,tan∠FED=
(2012•湛江二模)要制作一个如图的框架(单位:米),要求所围成的面积为6米2,其中ABCD是一个矩形,EFCD是一个等腰梯形,EF=3CD,tan∠FED=| 3 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
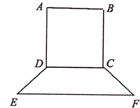 要制作一个如图的框架(单位:米),要求所围成的总面积为19.5(米2),其中ABCD是一个矩形,EFCD是一个等腰梯形,梯形高h=
要制作一个如图的框架(单位:米),要求所围成的总面积为19.5(米2),其中ABCD是一个矩形,EFCD是一个等腰梯形,梯形高h= AB,tan∠FED=
AB,tan∠FED= ,设AB=x米,BC=y米.
,设AB=x米,BC=y米.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省无锡市高三(上)期末数学试卷(解析版) 题型:解答题
 AB,tan∠FED=
AB,tan∠FED= ,设AB=x米,BC=y米.
,设AB=x米,BC=y米.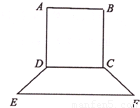
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com