Question

【题目】数列{an}的前n项和记为Sn且满足Sn=2an﹣1，n∈N*；
（1）求数列{an}的通项公式；
（2）设Tn=a1a2﹣a2a3+a3a4﹣a4a5+…+（﹣1）n+1anan+1 ， 求{Tn}的通项公式；
（3）设有m项的数列{bn}是连续的正整数数列，并且满足：lg2+lg（1+ ）+lg（1+ ）+…+lg（1+ ）=lg（log2am）．
问数列{bn}最多有几项？并求出这些项的和．

Answer 1

【答案】
（1）解：∵Sn=2an﹣1，n∈N*；∴n=1时，a1=S1=2a1﹣1，解得a1=1；

n≥2时，an=Sn﹣Sn﹣1=2an﹣1﹣（2an﹣1﹣1），

化为an=2an﹣1，∴数列{an}是等比数列，公比为2，首项为1．∴an=2n﹣1

（2）解：anan+1=2n﹣12n= ．

∴Tn=a1a2﹣a2a3+a3a4﹣a4a5+…+（﹣1）n+1anan+1

= +…+（﹣1）n+1×4n]

= = [1﹣（﹣4）n]

（3）解：由lg2+lg（1+ ）+lg（1+ ）+…+lg（1+ ）=lg（log2am）．

∴ × ×…× =log2am=m﹣1．

又数列{bn}是连续的正整数数列，∴bn=bn﹣1+1．

∴ =m﹣1，又bm=b1+（m﹣1），

∴mb1﹣3b1﹣2m=0，

∴m= =3+ ，由m∈N*，

∴b1＞2，∴b1=3时，m的最大值为9．

∴这些项的和=3+4+…+11=63

【解析】（1）Sn=2an﹣1，n∈N*；n=1时，a1=S1=2a1﹣1，解得a1；n≥2时，an=Sn﹣Sn﹣1 ， 化为an=2an﹣1 ， 利用等比数列的通项公式即可得出．（2）anan+1=2n﹣12n= ．利用等比数列的求和公式即可得出．（3）由lg2+lg（1+ ）+lg（1+ ）+…+lg（1+ ）=lg（log2am）．可得 × ×…× =log2am=m﹣1．又数列{bn}是连续的正整数数列，bn=bn﹣1+1．化简进而得出．
【考点精析】根据题目的已知条件，利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案，需要掌握数列{an}的前n项和sn与通项an的关系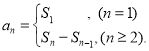；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．