
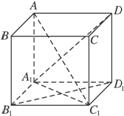
(1)B1D1与A1D能否垂直?请证明你的判断.
(2)当∠A1B1C1在[![]() ,
,![]() ]上变化时,求异面直线AC1与A1B1所成角的取值范围.
]上变化时,求异面直线AC1与A1B1所成角的取值范围.
解析:(1)不可能垂直.
如果B1D1⊥A1D则B1D1⊥A1D1(三垂线定理逆定理).
而这不可能.∴B1D1不垂直于A1D.
(2)解法一:设![]() =a,
=a,![]() =b,
=b,![]() =c,则
=c,则
![]() =
=![]() -
-![]() =
=![]() -(
-(![]() +
+![]() )=a-(b+c).
)=a-(b+c).
![]() ·
·![]() =(a-b-c)·(-b)=b2+b·c-a·b
=(a-b-c)·(-b)=b2+b·c-a·b
=1-1×1cosθ=1-cosθ.
|![]() |=
|=![]() .
.
|![]() |=1
|=1
∴cos<![]() ,
,![]() >=
>=![]() ,0≤cosθ≤
,0≤cosθ≤![]() ,
,
∴![]() ≤cos<
≤cos<![]() ,
,![]() >≤
>≤![]() .
.
故AC1,与A1B1所成角范围[arccos![]() ,arccos
,arccos![]() ].
].
解法二:∵A1B1∥C1D1,
∴C1D1与AC1所成的角∠AC1D就是异面直线AC1与A1B1所成的角.
∵![]() ≤∠A1B1C1≤
≤∠A1B1C1≤![]() ,
,
∴0≤cosA1B1C1≤![]() .
.
在△A1B1C1中
A1C12=B1C12+A1B12-2B1C1·A1B1
cosA1B1C1
=1+1-2cosA1B1C1
=2-2cosA1B1C1.
在Rt△AA1C1中,
AC12=AA12+A1C12=22+A1C12=4+A1C12.
连结AD1在,Rt△AA1D中,AD12=AA12+A1D12=22+12=5.
在△AC1D1中,
cosAC1D1=![]()
=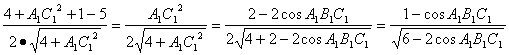 .
.
∵0≤cosA1B1C1≤![]() ,
,
∴![]() ≤cosAC1D≤
≤cosAC1D≤![]() .
.
故AC1与A1B1所成的角范围为?[arccos![]() ,arccos
,arccos![]() ].
].


科目:高中数学 来源: 题型:
 18、如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点,F为AB的中点.证明:
18、如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点,F为AB的中点.证明:查看答案和解析>>
科目:高中数学 来源: 题型:
 18、如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点.
18、如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 15、如图,在直四棱柱ABCD-A1B1C1D1中,A1C1⊥B1D1,E,F分别是AB,BC的中点.
15、如图,在直四棱柱ABCD-A1B1C1D1中,A1C1⊥B1D1,E,F分别是AB,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1,F分别是棱AD,AA1,AB的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1,F分别是棱AD,AA1,AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2010•抚州模拟)如图,在直四棱柱ABCD-A1B1C1D1中,AB=BC,∠ABC=60°,BB1=BC=2,M为BC中点,点N在CC1上.
(2010•抚州模拟)如图,在直四棱柱ABCD-A1B1C1D1中,AB=BC,∠ABC=60°,BB1=BC=2,M为BC中点,点N在CC1上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com