
【题目】如图,在四棱柱![]() 中;
中;
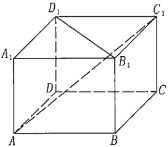
已知三个论断:(1)四棱柱![]() 是直四棱柱;(2)底面
是直四棱柱;(2)底面![]() 是菱形;(3)
是菱形;(3)![]() .
.
以其中两个论断作条件,余下一个为结论,可以得到三个命题,其中有几个是真命题?说明理由.
【答案】1个;理由见解析
【解析】
分别写出三个命题然后逐一判断.
解:以(1)、(2)作为条件,(3)为结论:即![]() 为直四棱柱,底面为菱形,则侧棱
为直四棱柱,底面为菱形,则侧棱![]() 底面.
底面.
∴![]() 在上底面上的射影为
在上底面上的射影为![]() .又底面为菱形,∴
.又底面为菱形,∴![]() .
.
由三垂线定理得![]() ,这一命题为真.
,这一命题为真.
以(2)、(3)为条件,(1)为结论:![]()
![]() 为菱形,∴
为菱形,∴![]() .
.
又![]() ,∴
,∴![]() 平面
平面![]() .∴
.∴![]() .
.
但侧棱![]() 未必垂直于底面.事实上,若侧棱倾斜,但保持与
未必垂直于底面.事实上,若侧棱倾斜,但保持与![]() 垂直(这是可以做到的),则必符合条件(2)、(3),故此四棱柱不一定是直四棱柱.
垂直(这是可以做到的),则必符合条件(2)、(3),故此四棱柱不一定是直四棱柱.
若(1)、(3)为条件,(2)为结论:![]()
![]() 在底面
在底面![]() 上的射影为
上的射影为![]() ,又
,又![]() ,由三垂线定理的逆定理得
,由三垂线定理的逆定理得![]() ,即四边形
,即四边形![]() 的对角线互相垂直,但这样的四边形未必是菱形.
的对角线互相垂直,但这样的四边形未必是菱形.
由以上分析知,真命题只有1个,即(1)(2)![]() (3).
(3).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】若存在常数![]() ,使对任意的
,使对任意的![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 为
为![]() 数列.
数列.
(1)已知![]() 是公差为2的等差数列,其前n项和为
是公差为2的等差数列,其前n项和为![]() .若
.若![]() 是
是![]() 数列,求
数列,求![]() 的取值范围;
的取值范围;
(2)已知数列![]() 的各项均为正数,记数列
的各项均为正数,记数列![]() 的前n项和为
的前n项和为![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() .
.
①求证:数列![]() 是等比数列;
是等比数列;
②设![]() ,试证明:存在常数
,试证明:存在常数![]() ,对于任意的
,对于任意的![]() ,数列
,数列![]() 都是
都是![]() 数列.
数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气的晷长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长减少或增加的量相同,周而复始.已知每年冬至的晷长为一丈三尺五寸,夏至的晷长为一尺五寸(一丈等于十尺,一尺等于十寸),则说法不正确的是( )
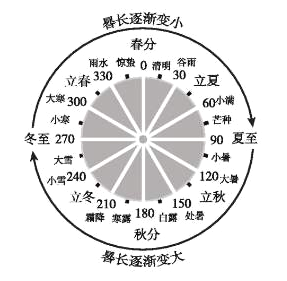
A.相邻两个节气晷长减少或增加的量为一尺
B.春分和秋分两个节气的晷长相同
C.立冬的晷长为一丈五寸
D.立春的晷长比立秋的晷长短
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资人打算投资甲、乙两个项目,根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损率分别为30%和10%,投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元,问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直角梯形ABCD中,![]() ,
,![]() ,
,![]() ,将直角梯形ABCD(及其内部)以AB所在直线为轴顺时针旋转90°,形成如图所示的几何体,其中M为
,将直角梯形ABCD(及其内部)以AB所在直线为轴顺时针旋转90°,形成如图所示的几何体,其中M为![]() 的中点.
的中点.
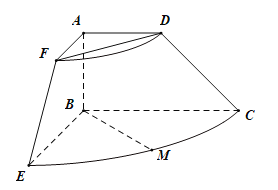
(1)求证:![]() ;
;
(2)求异面直线BM与EF所成角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com