
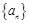 各项均不为0,其前
各项均不为0,其前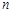 项和为
项和为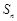 ,且对任意
,且对任意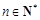 都有
都有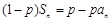 (
(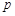 为大于1的常数),记
为大于1的常数),记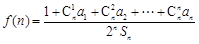 .
.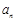 ;
;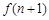 与
与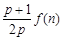 的大小(
的大小(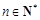 );
);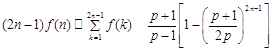
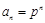 (2)由(1)可得
(2)由(1)可得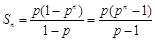 ,结合整体思想来得到比较大小
,结合整体思想来得到比较大小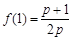 ,
,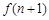
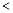
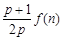 ,(
,(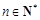 ).结合放缩法来得到证明。
).结合放缩法来得到证明。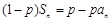 ,① ∴
,① ∴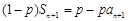 .②
.②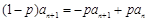 ,即
,即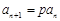 . (3分) 在①中令
. (3分) 在①中令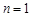 ,
,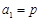 .∴
.∴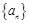 是首项为
是首项为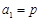 ,公比为
,公比为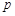 的等比数列,
的等比数列,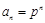 . (4分)
. (4分)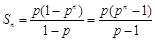 .
.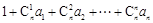
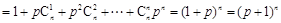 .
.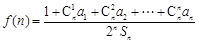
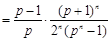 , (5分)
, (5分)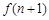
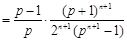 .而
.而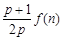
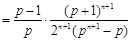 ,且
,且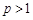 ,
,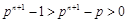 ,
,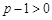 .∴
.∴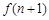
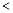
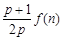 ,(
,(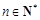 ).(8分)
).(8分)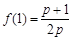 ,
,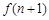
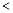
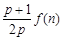 ,(
,(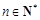 ).
).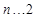 时,
时,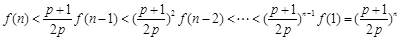 .
.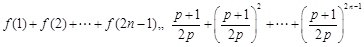
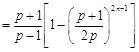 ,(10分)(当且仅当
,(10分)(当且仅当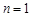 时取等号).
时取等号).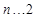 ,
,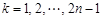 时,
时,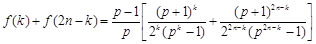
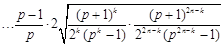
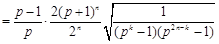
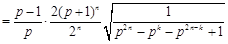 .
.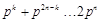 ,∴
,∴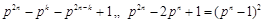 .
.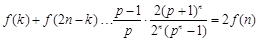 ,(当且仅当
,(当且仅当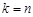 时取等号).(13分)
时取等号).(13分)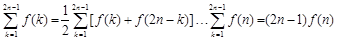 .(当且仅当
.(当且仅当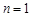 时取等号).
时取等号).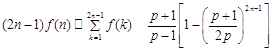 ,(
,(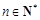 ).(14分)
).(14分)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com