
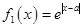 ,
,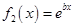 .
.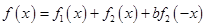 ,是否存在
,是否存在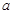 、
、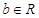 ,使
,使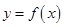 为偶函数,如果存在,请举例并证明你的结论,如果不存在,请说明理由;
为偶函数,如果存在,请举例并证明你的结论,如果不存在,请说明理由;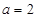 ,
,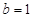 ,求
,求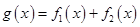 在
在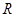 上的单调区间;
上的单调区间;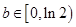 ,
,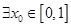 对
对 ,,有
,,有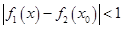 成立,求
成立,求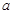 的取值范围.
的取值范围.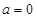 ,
,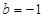 ;(2)函数
;(2)函数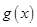 的增区间为
的增区间为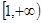 ,减区间为
,减区间为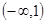 ;
; 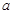 的取值范围是
的取值范围是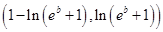 .
. ,
, 代入函数
代入函数 的解析式,去绝对值符号,将函数
的解析式,去绝对值符号,将函数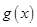 的解析式利用分段函数的形式表示出来,然后利用导数求出函数
的解析式利用分段函数的形式表示出来,然后利用导数求出函数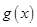 在相应区间上的单调区间;(3)先将绝对值符号去掉,得到
在相应区间上的单调区间;(3)先将绝对值符号去掉,得到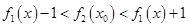 ,并根据题中的意思将问题转化为
,并根据题中的意思将问题转化为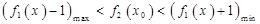 ,然后利用导数进行求解,从而求出参数
,然后利用导数进行求解,从而求出参数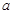 的取值范围.
的取值范围.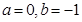 使
使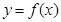 为偶函数,证明如下:
为偶函数,证明如下: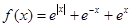 ,
,  ,
,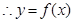 为偶函数,
为偶函数,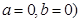
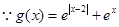 ,
,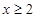 时
时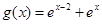 ,
,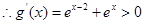 ,
,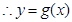 在
在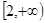 上为增函数,
上为增函数,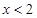 时
时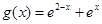 ,
,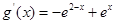 ,令
,令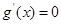 则
则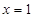 ,
,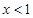 时
时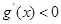 ,
,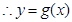 在
在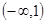 上为减函数,
上为减函数,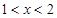 时
时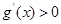 ,
,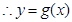 在
在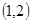 上为增函数,
上为增函数,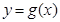 的增区间为
的增区间为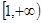 ,减区间为
,减区间为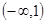 ;
; 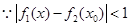 ,
,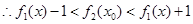
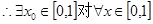 ,
,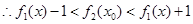 成立。
成立。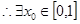
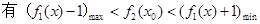
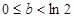 时,
时,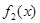 为增函数或常数函数,
为增函数或常数函数,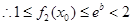
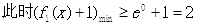
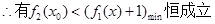
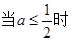
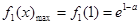
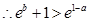
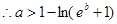
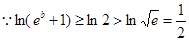
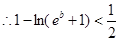
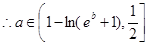
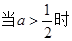
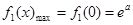
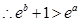
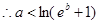
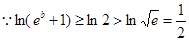
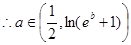
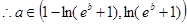 .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com