【答案】
分析:(1)先求函数的定义域,然后求出导函数,讨论a的正负,再结合导函数的符号可得函数f(x)的单调区间;
(2)用分析法进行证明,要证明:
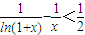
在(0,1)上成立,只需证:
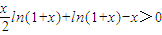
,在(0,1)上恒成立,设
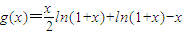
,然后利用导数研究函数g(x)在(0,1)上单调性,可得结论.
解答:解:(1)由
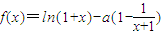
知定义域:{x|x>-1}
对f(x)求导得:
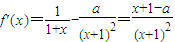
①在a≤0时,有x+1-a>0恒成立.故f(x)>0
故此时f(x)在(-1,+∞)上单调递增
②在a>0时,由f'(x)=0知x=a-1
| x | (-1,a-1) | a-1 | (a-1,+∞) |
| f'(x) | - | | + |
| f(x) | ↓ | 极小值 | ↑ |
故在a>0时,f(x)在(-1,a-1)上为减函数,在[a-1,+∞)上为增函数.
因此函数在a≤0时,在(-1,+∞)上单调递增;在a>0时,f(x)在(-1,a-1)上为减函数,在[a-1,+∞)上为增函数.…(5分)
(2)要证明:
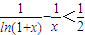
在(0,1)上成立.
只需证:
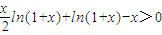
,在(0,1)上恒成立
设
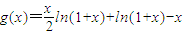
则
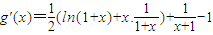
=
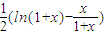
由(1)可知a=1,f(x)在x=0时取到最小值
有
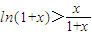
,在x>0时恒成立.
从而可知g'(x)>0,故g(x)在(0,1)上为增函数∴g(x)>g(0)=0
即:
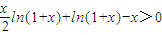
恒成立,从而原不等式得证.…(12分)
点评:本题主要考查了函数恒成立问题,以及利用导数研究函数单调性,同时考查了转化能力,属于中档题.

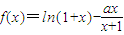 (其中a为常数),求函数f(x)的单调区间;
(其中a为常数),求函数f(x)的单调区间;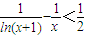 在0<x<1上恒成立.
在0<x<1上恒成立.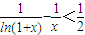 在(0,1)上成立,只需证:
在(0,1)上成立,只需证: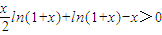 ,在(0,1)上恒成立,设
,在(0,1)上恒成立,设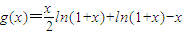 ,然后利用导数研究函数g(x)在(0,1)上单调性,可得结论.
,然后利用导数研究函数g(x)在(0,1)上单调性,可得结论.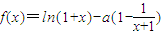 知定义域:{x|x>-1}
知定义域:{x|x>-1}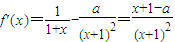
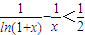 在(0,1)上成立.
在(0,1)上成立.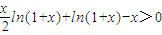 ,在(0,1)上恒成立
,在(0,1)上恒成立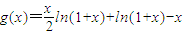
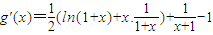 =
=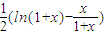
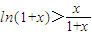 ,在x>0时恒成立.
,在x>0时恒成立.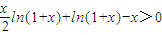 恒成立,从而原不等式得证.…(12分)
恒成立,从而原不等式得证.…(12分)
