
(1)证明AC⊥SB;
(2)求二面角N—CM—B的余弦值;
(3)求点B到平面CMN的距离.
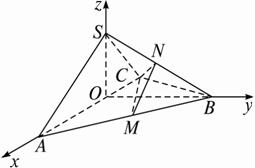
思路分析:由题目所给的条件,恰当地建立空间直角坐标系,由空间向量的坐标表示的内容进行证明、求解即可.
解:(1)证明如下,取AC中点O,连结OS、OB.
∵SA=SC,BA=BC,
∴AC⊥SO且AC⊥BO.
∵平面SAC⊥平面ABC,平面SAC∩平面ABC=AC,
∴SO⊥面ABC.∴SO⊥BO.
如图所示建立空间直角坐标系O-xyz.

则A(2,0,0),C(-2,0,0),S(0,0,2),B(0,![]() ,0).∴
,0).∴![]() =(-4,0,0),
=(-4,0,0),![]() =(0,-
=(0,-![]() ,2),∵
,2),∵![]() ·
·![]() =(-4,0,0)·(0,-
=(-4,0,0)·(0,-![]() ,2)=0,
,2)=0,
∴AC⊥BS.
(2)解:由(1),得M(1,![]() ,0),
,0),![]() =(3,
=(3,![]() ,0),
,0),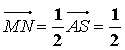 (-2,0,2)=(-1,0,1).
(-2,0,2)=(-1,0,1).
设n=(x,y,z)为平面CMN的一个法向量,则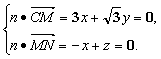
取x=-1,y=![]() ,z=-1,则n=(-1,
,z=-1,则n=(-1,![]() ,-1),
,-1),
又![]() =(0,0,2)为平面ABC的一个法向量,
=(0,0,2)为平面ABC的一个法向量,
∴cos〈n,![]() 〉=
〉= .
.
∴二面角N-CM-B的余弦值为![]() .
.
(3)解:由(1)(2),得![]() =(2,
=(2,![]() ,0).n=(-1,
,0).n=(-1,![]() ,-1)为平面CMN的一个法向量.∴点B到平面CMN的距离d=
,-1)为平面CMN的一个法向量.∴点B到平面CMN的距离d= .
.


科目:高中数学 来源: 题型:
 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为1的等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为1的等边三角形,∠BAC=90°,O为BC中点.查看答案和解析>>
科目:高中数学 来源: 题型:
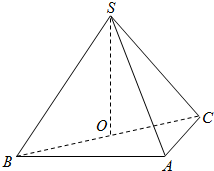 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,AC=2
如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,AC=2| 3 |
| 2S |
| l |
 C.
C.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2S |
| l |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在三棱锥S-ABC中,SA=AB=BC=AC=
如图,在三棱锥S-ABC中,SA=AB=BC=AC=| 2 |
| 2 |
| ||
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com