
(本小题12分)
已知函数
 是奇函数,且
是奇函数,且
(1)求 ,
, 的值;
的值;
(2)用定义证明 在区间
在区间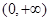 上是减函数.
上是减函数.
(1)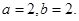 ;(2)见解析。
;(2)见解析。
【解析】
试题分析:(1)由题意知, ,所以
,所以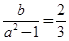 ①
①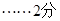
因为函数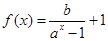 是奇函数,所以
是奇函数,所以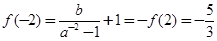 ,
,
所以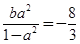 ②
②
由①②可得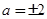 (
(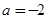 舍去),所以
舍去),所以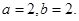
(2)由(1)可得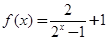 ,设
,设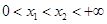 ,则
,则
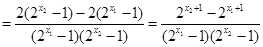
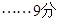
因为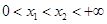 ,且
,且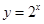 在
在 为增函数,
为增函数,
所以 ,
, ,所以
,所以 ,
,
所以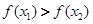 ,所以
,所以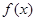 在区间
在区间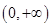 上是减函数
上是减函数
考点:本题主要考查利用函数的奇偶性求参数值及利用定义证明函数的单调性.
点评:已知一个函数为奇函数,如果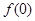 有意义,则
有意义,则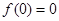 ,这个条件非常好用,常常能使运算变得非常简单;用定义法证明函数单调性时,要严格按照函数单调性的定义,遵循设变量、作差、变形、判断符号、下结论等步骤进行证明,另外需要注意的是变形时要化到最简单的形式,不要用已知函数的单调性来证明未知函数的单调性.用定义法证明函数的单调性是一个非常重要的考点,学生应该注意牢固掌握,灵活应用.
,这个条件非常好用,常常能使运算变得非常简单;用定义法证明函数单调性时,要严格按照函数单调性的定义,遵循设变量、作差、变形、判断符号、下结论等步骤进行证明,另外需要注意的是变形时要化到最简单的形式,不要用已知函数的单调性来证明未知函数的单调性.用定义法证明函数的单调性是一个非常重要的考点,学生应该注意牢固掌握,灵活应用.


科目:高中数学 来源:2010-2011学年福建师大附中高三上学期期中考试理科数学卷 题型:解答题
(本小题12分)已知函数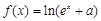 (
( 为常数)是实数集
为常数)是实数集 上的奇函数,函数
上的奇函数,函数 是区间[-1,1]上的减函数.
是区间[-1,1]上的减函数.
(I)求 的值;
的值;
(II)若 在
在 及
及 所在的取值范围上恒成立,求
所在的取值范围上恒成立,求 的取值范围;
的取值范围;
(Ⅲ)讨论关于 的方程
的方程 的根的个数.
的根的个数.
查看答案和解析>>
科目:高中数学 来源:2010年吉林省高一上学期期中考试数学试卷 题型:解答题
(本小题12分)已知二次函数 满足
满足 且
且 .
.
(1)求 的解析式;
的解析式;
(2) 当 时,不等式:
时,不等式: 恒成立,求实数
恒成立,求实数 的范围.
的范围.
(3)设
 ,求
,求 的最大值;
的最大值;
查看答案和解析>>
科目:高中数学 来源:2010-2011年福建省高二下学期期中考试理科数学 题型:解答题
(本小题12分)
已知双曲线的中心在原点,左右焦点分别为 ,离心率为
,离心率为 ,且过点
,且过点 ,
,

(1)求此双曲线的标准方程;
(2)若直线系 (其中
(其中 为参数)所过的定点
为参数)所过的定点 恰在双曲线上,求证:
恰在双曲线上,求证: 。
。
查看答案和解析>>
科目:高中数学 来源:2010-2011年福建省四地六校高二下学期第一次月考数学文卷 题型:解答题
(本小题12分)
已知椭圆C的左右焦点坐标分别是(-1,0),(1, 0),离心率 ,直线
,直线 与椭圆C交于不同的两点M,N,以线段MN为直径作圆P。
与椭圆C交于不同的两点M,N,以线段MN为直径作圆P。
(1)求椭圆C的方程;
(2)若圆P恰过坐标原点,求圆P的方程;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com