
【题目】已知三棱台ABC﹣A1B1C1中,平面BB1C1C⊥平面ABC,∠ACB=90°,BB1=CC1=B1C1=2,BC=4,AC=6 
(1)求证:BC1⊥平面AA1C1C
(2)点D是B1C1的中点,求二面角A1﹣BD﹣B1的余弦值.
【答案】
(1)证明:梯形BB1C1C中,BB1=CC1=B1C1=2,BC=4得: ![]() ,从而BC1⊥CC1,
,从而BC1⊥CC1,
因为平面BB1C1C⊥平面ABC,且AC⊥BC,
所以AC⊥平面BB1C1C,因此BC1⊥AC,
因为AC∩CC1=C,所以BC1⊥平面AA1C1C
(2)解:如图,以CA,CB所在直线分别为x轴,y轴,点C为原点建立空间直角坐标系,则A(6,0,0),B(0,4,0),C(0,0,0),C1(0,1, ![]() ),B1(0,3,
),B1(0,3, ![]() ),D(0,2,
),D(0,2, ![]() ),A1(3,1,
),A1(3,1, ![]() ),
),
平面BB1D的法向量 ![]() =(1,0,0),设平面AB1D的法向量为
=(1,0,0),设平面AB1D的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 ![]() ,
,
令z= ![]() ,得
,得 ![]() (
( ![]() ,
, ![]() ),
),
所以所求二面角的余弦值是﹣  =﹣
=﹣ ![]() .
.

【解析】(1)证明BC1⊥CC1 , BC1⊥AC,即可证明BC1⊥平面AA1C1C(2)以CA,CB所在直线分别为x轴,y轴,点C为原点建立空间直角坐标系,求出平面的法向量,即可求二面角A1﹣BD﹣B1的余弦值.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ).
).
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值和最小值;
上的最大值和最小值;
(2)当![]() 时,是否存在正实数
时,是否存在正实数![]() ,当
,当![]() (
(![]() 是自然对数底数)时,函数
是自然对数底数)时,函数![]() 的最小值是3,若存在,求出
的最小值是3,若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
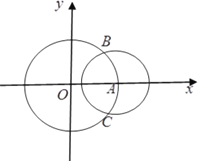
【题目】如图,在平面直角坐标系![]() 中,圆
中,圆![]() :
:![]() 与
与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,以点
,以点![]() 为圆心的圆
为圆心的圆![]() :
:![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)当![]() 时,求
时,求![]() 的长;
的长;
(2)当![]() 变化时,求
变化时,求![]() 的最小值;
的最小值;
(3)过点![]() 的直线
的直线![]() 与圆A切于点
与圆A切于点![]() ,与圆
,与圆![]() 分别交于点
分别交于点![]() ,
,![]() ,若点
,若点![]() 是
是![]() 的中点,试求直线
的中点,试求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近几年,京津冀等地数城市指数“爆表”,尤其2015年污染最重.为了探究车流量与PM2.5的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与PM2.5的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
车流量x(万辆) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
PM2.5的浓度y(微克/立方米) | 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(Ⅰ)由散点图知y与x具有线性相关关系,求y关于x的线性回归方程;
(Ⅱ)(ⅰ)利用(Ⅰ)所求的回归方程,预测该市车流量为8万辆时PM2.5的浓度;
(ⅱ)规定:当一天内PM2.5的浓度平均值在(0,50]内,空气质量等级为优;当一天内PM2.5的浓度平均值在(50,100]内,空气质量等级为良.为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数.)
参考公式:回归直线的方程是![]() ,其中
,其中 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() 的首项
的首项![]() ,且满足
,且满足![]() ,
,![]() ,其中
,其中![]() ,设数列
,设数列![]() ,
,![]() 的前项和分别为
的前项和分别为![]() ,
,![]() .
.
(Ⅰ)若不等式![]() 对一切
对一切![]() 恒成立,求
恒成立,求![]() .
.
(Ⅱ)若常数![]() 且对任意的
且对任意的![]() ,恒有
,恒有![]() ,求
,求![]() 的值.
的值.
(Ⅲ)在(Ⅱ)的条件下且同时满足以下两个条件:
(ⅰ)若存在唯一正整数![]() 的值满足
的值满足![]() ;
;
(ⅱ)![]() 恒成立.试问:是否存在正整数,使得
恒成立.试问:是否存在正整数,使得![]() ,若存在,求
,若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地棚户区改造建筑平面示意图如图所示,经规划调研确定,棚改规划建筑用地区域近似为圆面,该圆面的内接四边形![]() 是原棚户区建筑用地,测量可知边界
是原棚户区建筑用地,测量可知边界![]() 万米,
万米,![]() 万米,
万米,![]() 万米.
万米.
(1)请计算原棚户区建筑用地![]() 的面积及
的面积及![]() 的长;
的长;
(2)因地理条件的限制,边界![]() 不能更改,而边界
不能更改,而边界![]() 可以调整,为了提高棚户区建筑用地的利用率,请在圆弧
可以调整,为了提高棚户区建筑用地的利用率,请在圆弧![]() 上设计一点
上设计一点![]() ,使得棚户区改造后的新建筑用地
,使得棚户区改造后的新建筑用地![]() 的面积最大,并求出最大值.
的面积最大,并求出最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是![]() ,D是AC的中点。
,D是AC的中点。

(1)求证:B1C∥平面A1BD;
(2)求二面角A1-BD-A的大小;
(3)在线段AA1上是否存在一点E,使得平面B1C1E⊥平面A1BD,若存在,求出AE的长;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中(![]() 为坐标原点),已知两点
为坐标原点),已知两点![]() ,
,![]() ,且三角形
,且三角形![]() 的内切圆为圆
的内切圆为圆![]() ,从圆
,从圆![]() 外一点
外一点![]() 向圆引切线
向圆引切线![]() ,
,![]() 为切点。
为切点。
(1)求圆![]() 的标准方程.
的标准方程.
(2)已知点![]() ,且
,且![]() ,试判断点
,试判断点![]() 是否总在某一定直线
是否总在某一定直线![]() 上,若是,求出直线
上,若是,求出直线![]() 的方程;若不是,请说明理由.
的方程;若不是,请说明理由.
(3)已知点![]() 在圆
在圆![]() 上运动,求
上运动,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com