【题目】下面有两个关于“袋子中装有红、白两种颜色的相同小球，从袋中无放回地取球”的游戏规则，这两个游戏规则公平吗？为什么？
游 戏 1 | 游 戏 2 |
2个红球和2个白球 | 3个红球和1个白球 |
取1个球，再取1个球 | 取1个球，再取1个球 |
取出的两个球同色→甲胜 | 取出的两个球同色→甲胜 |
取出的两个球不同色→乙胜 | 取出的两个球不同色→乙胜 |
【答案】规则是公平的.
【解析】本试题主要是考查了古典概型概率的求解，利用游戏规则，我们只需要判定甲胜的概率和乙胜的概率的大小即可。概率不一样就说明不公平。分别求解游戏1和游戏2中的胜出的概率值，我们可以判断游戏一不公平，游戏2公平。
解：游戏１：从2个红球和2个白球中，取1个球，再取1个球，基本事件共有12个.
“取出的两个球同色”包含的基本事件有４个. ……３分
所以Ｐ（甲胜）＝
，Ｐ（乙胜）＝１－
＝
.
因此规则是不公平的. ……５分
游戏２：从３个红球和１个白球中，取1个球，再取1个球，基本事件共有12个.
“取出的两个球同色”包含的基本事件有６个. ……８分
所以Ｐ（甲胜）＝
，Ｐ（乙胜）＝１－
＝
.
因此规则是公平的. ……10分
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案科目：高中数学 来源： 题型：
【题目】如图，四棱锥
中，底面
为梯形， 
底面
， 
.过
作一个平面
使得
平面
.
（1）求平面
将四棱锥
分成两部分几何体的体积之比；
（2）若平面
与平面
之间的距离为
，求直线
与平面
所成角的正弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥
中，已知
平面
，且四边形
为直角梯形， 
， 
， 
，点
， 
分别是
， 
的中点．
（I）求证： 
平面
；
（Ⅱ）点
是线段
上的动点，当直线
与
所成角最小时，求线段
的长．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列
为等比数列，
,公比为
，且
，
为数列的前
项和.
（1）若
，求
；
（2）若调换
的顺序后能构成一个等差数列，求的所有可能值；
（3）是否存在正常数
，使得对任意正整数，不等式
总成立？若存在，求出的范围，若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设a是从集合{1，2，3，4}中随机取出的一个数，b是从集合{1，2，3}中随机取出的一个数，构成一个基本事件（a，b）。记“在这些基本事件中，满足logba≥1为事件A，则A发生的概率是 ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知O为坐标原点，P为双曲线 
﹣y2=1（a＞0）上一点，过P作两条渐近线的平行线交点分别为A，B，若平行四边形OAPB的面积为 
，则双曲线的离心率为（ ）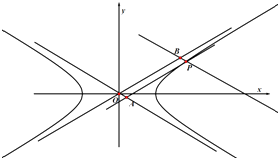
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设等差数列
的前
项和为
，在同一个坐标系中，
及
的部分图象如图所示，则（ ）．
A. 当
时，取得最大值 B. 当
时，取得最大值
C. 当时，取得最小值 D. 当时，取得最小值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
