
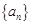 的前
的前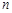 项和为
项和为 ,
,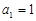 ,
,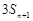 是
是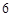 与
与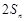 的等差中项(
的等差中项(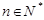 ).
).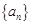 的通项公式;
的通项公式;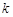 ,使不等式
,使不等式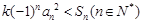 恒成立,若存在,求出
恒成立,若存在,求出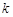
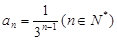 (2)存在,11
(2)存在,11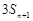 是
是 与
与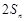 的等差中项,利用等差中项得到
的等差中项,利用等差中项得到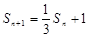 ,(
,(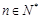 )①,
)①,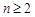 时有
时有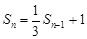 ②,则①-②可得
②,则①-②可得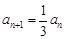 ,从而可得数列通项.
,从而可得数列通项.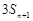 是
是 与
与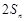 的等差中项,利用等差中项得到
的等差中项,利用等差中项得到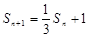 ,(
,(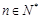 )①,根据该式的结构特征,利用构造法,可构造出等比数列
)①,根据该式的结构特征,利用构造法,可构造出等比数列 ,从而求得
,从而求得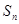 ,进而利用
,进而利用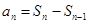 得到数列的通项.
得到数列的通项. 项和;代入
项和;代入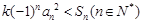 化简,讨论
化简,讨论 的奇偶发现,
的奇偶发现,  为奇数时,恒成立;
为奇数时,恒成立;  为偶数时,可将其转化为二次函数在固定区间恒成立问题,利用单调性可判断是否存在这样的正整数
为偶数时,可将其转化为二次函数在固定区间恒成立问题,利用单调性可判断是否存在这样的正整数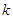 .
. 是
是 与
与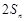 的等差中项,
的等差中项,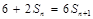 (
(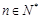 ),即
),即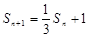 ,(
,(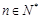 )①
)①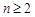 时有
时有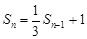 ②
②  ,即
,即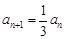 对
对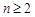 都成立
都成立 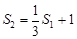 即
即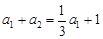 ,所以
,所以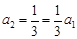
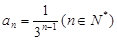 . 所以数列
. 所以数列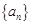 是首项为1,公比为
是首项为1,公比为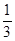 的等比数列.
的等比数列.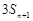 是
是 与
与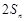 的等差中项,
的等差中项,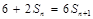 (
(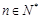 ),即
),即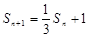 ,(
,(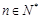 )
) (
(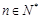 ),
),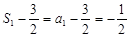 ,所以
,所以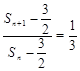 (
(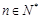 ),
), 是以
是以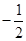 为首项,
为首项,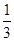 为公比的等比数列.
为公比的等比数列. 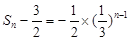 ,即
,即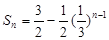 (
(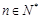 ),
),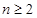 时,
时,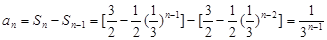 ,
, 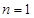 时,
时,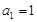 也适合上式,所以
也适合上式,所以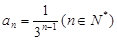 .
.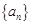 是首项为1,公比为
是首项为1,公比为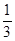 的等比数列,
的等比数列, 项和为
项和为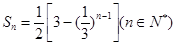 .
.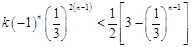 (
(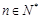 )①恒成立.
)①恒成立.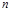 为奇数时,不等式左边恒为负数,右边恒为正数,所以对任意正整数
为奇数时,不等式左边恒为负数,右边恒为正数,所以对任意正整数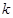 不等式恒成立;
不等式恒成立;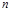 为偶数时,①等价于
为偶数时,①等价于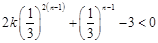 恒成立,
恒成立,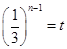 ,有
,有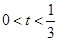 ,则①等价于
,则①等价于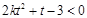 在
在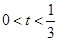 恒成立,
恒成立, 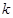 为正整数,二次函数
为正整数,二次函数 的对称轴显然在
的对称轴显然在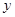 轴左侧,
轴左侧,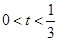 时,二次函数为增函数,故只须
时,二次函数为增函数,故只须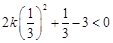 ,解得
,解得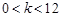 ,
,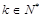 ,
,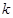 ,且其最大值为11.
,且其最大值为11.  求通项;构造等比数列法;分类讨论;二次函数在固定区间恒成立.
求通项;构造等比数列法;分类讨论;二次函数在固定区间恒成立.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com