练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】给定点，若是直线上位于第一象限内的一点，直线与轴的正半轴相交于点.试探究：的面积是否具有最小值?若有，求出点的坐标；若没有，则说明理由.若点为直线上的任意一点，情况又会怎样呢?

    【答案】的面积存在最小值为，此时 ，若为直线上的任意一点时，的面积不具有最小值.

    【解析】

    设出点的坐标，根据三点共线，求得参数之间的关系，将问题转化为求函数的最小值；根据方程有根，用判别式法求得参数范围以及面积的最值.

    依题意画草图如图：

    设

    由三点共线得

    解得

    而的面积

    问题转化为求函数的最小值.

    函数的定义域为

    将函数式变形为 （※）

    （※）方程有根

    即

    解得或（舍，）

    的面积存在最小值为，此时

    若为直线上的任意一点时，的面积不具有最小值.

    当无限地接近于原点时，的面积无限地接近于.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】[选修4-4：坐标系与参数方程]

    在平面直角坐标系中，直线的参数方程为（为参数），在以直角坐标系的原点为极点， 轴的正半轴为极轴的极坐标系中，曲线的极坐标方程为.

    （Ⅰ）求曲线的直角坐标方程和直线的普通方程；

    （Ⅱ）若直线与曲线相交于， 两点，求的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合M＝{x|x<－3，或x>5}，P＝{x|(x－a)·(x－8)≤0}．

    (1)求M∩P＝{x|5<x≤8}的充要条件；

    (2)求实数a的一个值，使它成为M∩P＝{x|5<x≤8}的一个充分但不必要条件．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，且过点．

    （Ⅰ）求椭圆的方程．

    （Ⅱ）若， 是椭圆上两个不同的动点，且使的角平分线垂直于轴，试判断直线的斜率是否为定值？若是，求出该值；若不是，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （Ⅰ）若,求曲线在点处的切线方程;

    （Ⅱ）若,求函数的单调区间;

    （Ⅲ）若,求证: .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设数列{}是等差数列，数列{}的前项和满足,,且

    （1）求数列{}和{}的通项公式：

    （2）设为数列{．}的前项和，求．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知{xn}是各项均为正数的等比数列，且x1＋x2＝3，x3－x2＝2.

    (1)求数列{xn}的通项公式；

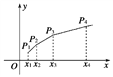
    (2)如图，在平面直角坐标系xOy中，依次连接点P1(x1,1)，P(x2,2)，…，Pn＋1(xn＋1，n＋1)得到折线P1P2…Pn＋1，求由该折线与直线y＝0，x＝x1，x＝xn＋1所围成的区域的面积Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆（）的上顶点与抛物线（）的焦点重合.

    （1）设椭圆和抛物线交于， 两点，若，求椭圆的方程；

    （2）设直线与抛物线和椭圆均相切，切点分别为， ，记的面积为，求证： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为进一步贯彻落实“十九”大精神，某高校组织了“歌颂祖国，紧跟党走”为主题的党史知识竞赛,从参加竞赛的学生中，随机抽取40名学生，将其成绩分为六段，，，得到如图所示的频率分布直方图.

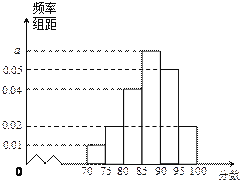
    （1）求图中的值；

    （2）若从竞赛成绩在与两个分数段的学生中随机选取两名学生，设这两名学生的竞赛成绩之差的绝对值不大于分为事件,求事件发生的概率.

    查看答案和解析>>

    同步练习册答案