解:(1)∵lga-lgc=lgsinB=-lg

∴

∴
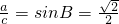
∵B为锐角,∴
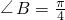
,
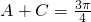
由正弦定理可得,

,
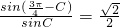
整理可得cosC=0∴

∴△ABC为等腰直角三角形
(2)∵sinA=2cosCsinB
由正弦定理及余弦定理可得,a=b×
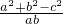
化简可得,b=c
所以△ABC为等腰三角形
(3)∵A、B、C成等差数列,∴A+C=2B,从而可得A+C=

,B=

∵a、b、c成等比数列∴b
2=ac
由正弦定理可得
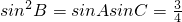
∴
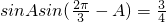
∴sinA
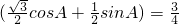
,
整理可得
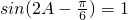
,则B=C=

,
∴三角形△ABC为等边三角形
(4)∵acosB+bcosC+ccosA=bcosA+ccosB+acosC
由余弦定理可得
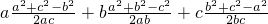
=
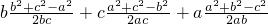
整理可得

∴

整理可得

∴a=b=c
三角形△ABC为等边三角形
(5)由已知可得,a
3+b
3-c
3=ac
2+bc
2-c
3∴(a+b)(a
2-ab+b
2)=(a+b)c
2∴a
2+b
2-c
2=ab
由余弦定理可得

,∴

,
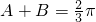
∵

∴sinA
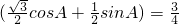
,
整理可得
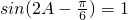
,则B=C=

,
三角形△ABC为等边三角形
(6)(a
2+b
2)sin(A-B)=(a
2-b
2)sin(A+B)
可得a
2[sin(A-B)-sin(A+B)]+b
2[sin(A-B)+sin(A+B)]=0
a
2sinBcosA=b
2sinAcosB
由正弦定理sin
2AsinBcosA=sin
2BsinAcosB
整理可得sin2A=sin2B,从而可得2A=2B或2A+2B=π
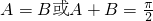
∴三角形△ABC为等腰三角形或直角三角形
分析:(1)先由对数的运算性质化简,可得
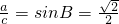
,从而可求B,再利用正弦定理代入可求A,C
(2)利用正弦、余弦定理化简可得
(3))∵A、B、C成等差数列,∴A+C=2B,从而可得A+C=

,B=

,由a、b、c成等比数列可得b
2=ac,结合已知及正弦定理可求
(4)利用余弦定理可得由余弦定理可得
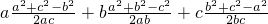
=
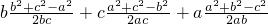
整理可得
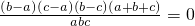
,从 而可得a=b=c
(5)先把已知整理可得,a
2+b
2-c
2=ab,利用余弦定理可求C,及A+B,再由
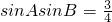
代入可求
(6))由(a
2+b
2)sin(A-B)=(a
2-b
2)sin(A+B)可得a
2[sin(A-B)-sin(A+B)]+b
2[sin(A-B)+sin(A+B)]=0
整理可得sin2A=sin2B,从而可得
点评:本题主要考查了利用正弦定理、余弦定理综合解三角形,判断三角形的形状,还考查了三角函数的公式,属于对基本知识的求解,但要体会在化简中的技巧.

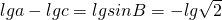 (B为锐角);
(B为锐角);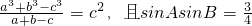 ;
;
 ∴
∴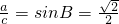
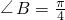 ,
,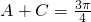
 ,
,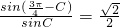

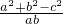
 ,B=
,B=
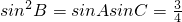
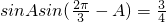 ∴sinA
∴sinA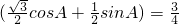 ,
,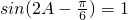 ,则B=C=
,则B=C= ,
,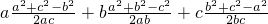 =
=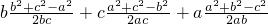



 ,∴
,∴ ,
,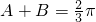

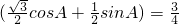 ,
,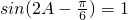 ,则B=C=
,则B=C= ,
,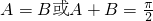
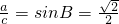 ,从而可求B,再利用正弦定理代入可求A,C
,从而可求B,再利用正弦定理代入可求A,C ,B=
,B= ,由a、b、c成等比数列可得b2=ac,结合已知及正弦定理可求
,由a、b、c成等比数列可得b2=ac,结合已知及正弦定理可求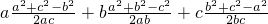 =
=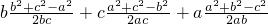
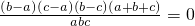 ,从 而可得a=b=c
,从 而可得a=b=c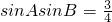 代入可求
代入可求
