
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若函数![]() 上是减函数,求实数a的最小值;
上是减函数,求实数a的最小值;
(Ⅲ)若![]() ,
,![]() ,使
,使![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
【答案】(1) 增区间是![]() 减区间是
减区间是![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:(1)先求导数,再求导函数零点,根据零点分类讨论导函数符号,确定单调区间(2)即等价于导函数![]() 上恒非正,利用变量分离,转化为对应函数最值:
上恒非正,利用变量分离,转化为对应函数最值:![]() 最大值,再利用导数研究函数
最大值,再利用导数研究函数![]() 最大值,即得实数a的取值范围,进而有最小值(3)等价于
最大值,即得实数a的取值范围,进而有最小值(3)等价于![]() ,由前两题不难得到
,由前两题不难得到![]() ,
,![]() ,代入即得实数a的取值范围.
,代入即得实数a的取值范围.
试题解析:解:由已知函数![]() 的定义域均为
的定义域均为![]() ,且
,且![]() .
.
(Ⅰ)函数 当
当![]() 时,
时,![]() .所以函数
.所以函数![]() 的单调增区间是
的单调增区间是![]() 当
当![]() 且
且![]() 时,
时, ![]() .所以函数
.所以函数![]() 的单调减区间是
的单调减区间是![]()
(Ⅱ)∵![]() 在
在![]() 上单调递减,∴
上单调递减,∴ ![]() 恒成立,即
恒成立,即![]() 恒成立,设
恒成立,设![]() ,∵
,∵![]() ,∴当
,∴当![]() 时,
时,![]() ∴
∴![]()
Ⅱ)因f(x)在![]() 上为减函数,故
上为减函数,故![]() 在
在![]() 上恒成立. 所以当
上恒成立. 所以当![]() 时
时![]() 又
又![]()
![]() , 故当
, 故当![]() ,即
,即![]() 时,
时,![]() . 所以
. 所以![]() 于是
于是![]() ,故a的最小值为
,故a的最小值为![]() .
.
(Ⅲ)由已知得“当![]() 时,有
时,有![]() ”.由(Ⅱ),当
”.由(Ⅱ),当![]() 时,
时, ![]() , 由(Ⅰ),当
, 由(Ⅰ),当![]() 时,有
时,有![]() 所以有
所以有![]() 故
故![]()


科目:高中数学 来源: 题型:
【题目】已知向量m=(cosx,-1),n=![]() ,函数f(x)=(m+n)·m.
,函数f(x)=(m+n)·m.
(1)求函数f(x)的最小正周期;
(2)已知a,b,c分别为△ABC内角A,B,C的对边,A为锐角,a=1,c=![]() ,且f(A)恰是函数f(x)在
,且f(A)恰是函数f(x)在![]() 上的最大值,求A,b和△ABC的面积.
上的最大值,求A,b和△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在公差不为零的等差数列{an}中,已知a1=1,且a1,a2,a5依次成等比数列.数列{bn}满足bn+1=2bn-1,且b1=3.
(1)求{an},{bn}的通项公式;
(2)设数列![]() 的前n项和为Sn,试比较Sn与1-
的前n项和为Sn,试比较Sn与1-![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了制定合理的节电方案,供电局对居民用电情况进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:度),将数据按照![]() ,
,![]() 分成9组,制成了如图所示的频率直方图.
分成9组,制成了如图所示的频率直方图.
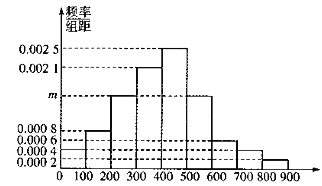
(1)求直方图中![]() 的值并估计居民月均用电量的中位数;
的值并估计居民月均用电量的中位数;
(2)从样本里月均用电量不低于700度的用户中随机抽取4户,用![]() 表示月均用电量不低于800度的用户数,求随机变量
表示月均用电量不低于800度的用户数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两支排球队进行比赛,约定先胜3局者获得比赛的胜利,比赛随即结束.除第五局甲队获胜的概率是![]() 外,其余每局比赛甲队获胜的概率都是
外,其余每局比赛甲队获胜的概率都是![]() .假设各局比赛结果相互独立.
.假设各局比赛结果相互独立.
(1)分别求甲队以3:0,3:1,3:2获胜的概率;
(2)若比赛结果为3:0或3:1,则胜利方得3分、对方得0分;若比赛结果为3:2,则胜利方得2分、对方得1分.求甲队得分X的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com