
 ,则直线l的方程为 .
,则直线l的方程为 .  ,可得MN=
,可得MN= BC=1.然后用直线方程的点斜式,分别求出直线AB、AC的方程,再令x=k,分别得到直线l与AB、AC的交点M、N坐标,最后用距离公式列式,可以得出k的值,从而得到直线l的方程.
BC=1.然后用直线方程的点斜式,分别求出直线AB、AC的方程,再令x=k,分别得到直线l与AB、AC的交点M、N坐标,最后用距离公式列式,可以得出k的值,从而得到直线l的方程. 解:∵B(4,1),C(4,4),
解:∵B(4,1),C(4,4), ,
,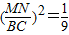 ⇒MN=
⇒MN= BC=1
BC=1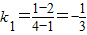
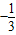 (x-1),即y=
(x-1),即y=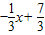
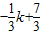 ,
,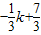 )
)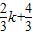 )
)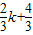 -(
-(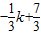 )=1⇒k=2
)=1⇒k=2

 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
在△ABC中,高线AD与BE的方程分别是x+5y-3=0和x+y-1=0,AB边所在直线的方程是x+3y-1=0,则△ABC的顶点坐标分别是A________;B________;C________.
查看答案和解析>>
科目:高中数学 来源:2012届广东北江中学第一学期期末考试高二文科数学 题型:填空题
已知△ABC的顶点坐标分别是A(1,2), B(-3,6), C(3,5), 则BC边上的高所在的直线方程
为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com