
【题目】已知数列{an}的前n项和为Sn , 且Sn=n﹣5an﹣85,n∈N+ .
(1)求an .
(2)求数列{Sn}的通项公式,并求出n为何值时,Sn取得最小值?并说明理由.(参考数据:lg 2≈0.3,lg 3≈0.48).
【答案】
(1)解:∵Sn=n﹣5an﹣85,∴当n=1时,S1=1﹣5a1﹣85,
即a1=1﹣5a1﹣85,解得a1=﹣14;
当n≥2时,an=Sn﹣Sn﹣1=(n﹣5an﹣85)﹣[(n﹣1)﹣5an﹣1﹣85]=﹣5an+5an﹣1+1,
整理得6an=5an﹣1+1,∴6(an﹣1)=5(an﹣1﹣1),
∴ ![]() =
= ![]() .又a1﹣1=﹣15,
.又a1﹣1=﹣15,
∴数列{an﹣1}是以﹣15为首项, ![]() 为公比的等比数列.
为公比的等比数列.
∴an=﹣15×( ![]() )n﹣1+1
)n﹣1+1
(2)解:由(1)知,an=﹣15×( ![]() )n﹣1+1,
)n﹣1+1,
代入Sn=n﹣5an﹣85得,Sn=n﹣5[﹣15×( ![]() )n﹣1+1]﹣85
)n﹣1+1]﹣85
=n+75×( ![]() )n﹣1﹣90.
)n﹣1﹣90.
设Sk为最小值,则 ![]() ,即有
,即有 ![]() ,
,
即 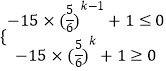 ,即
,即 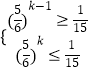 ,可得
,可得 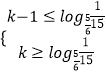 ,
,
即 ![]() ≤k≤
≤k≤ ![]() +1,又
+1,又 ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
lg2≈0.3,lg3≈0.48,∴ ![]() ≈14.75.
≈14.75.
∴14.75≤k≤15.75.又∵k∈N+,∴k=15.
即当n=15时,Sn取得最小值
【解析】(1)运用数列的通项与求和的关系:当n=1时,a1=S1 , 当n≥2时,an=Sn﹣Sn﹣1 , 通过构造数列,结合等比数列的定义和通项公式,即可得到所求;(2)将(1)的结论代入条件,可得Sn=n+75×( ![]() )n﹣1﹣90.设Sk为最小值,则
)n﹣1﹣90.设Sk为最小值,则 ![]() ,运用通项公式,结合对数函数的单调性,解不等式计算即可得到所求k的值.
,运用通项公式,结合对数函数的单调性,解不等式计算即可得到所求k的值.
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系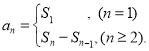 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】医院用甲、乙两种原料为手术后的病人配营养餐.甲种原料每10g含5单位蛋白质和10单位铁质,售价3元;乙种原料每10g含7单位蛋白质和4单位铁质,售价2元.若病人每餐至少需要35单位蛋白质和40单位铁质.试问:应如何使用甲、乙原料,才能既满足营养,又使费用最省.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的方程为3x+4y﹣12=0,求直线l'的方程,使得:
(1)l'与l平行,且过点(﹣1,3);
(2)l'与l垂直,且l'与两轴围成的三角形面积为4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动直线l:(m+3)x-(m+2)y+m=0与圆C:(x-3)2+(y-4)2=9.
(1)求证:无论m为何值,直线l总过定点A,并说明直线l与圆C总相交.
(2)m为何值时,直线l被圆C所截得的弦长最小?请求出该最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,已知
中,已知![]() 底面
底面![]() ,异面直线
,异面直线![]() 和
和![]() 所成角等于
所成角等于![]() .
.
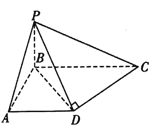
(1)求证: 平面![]() 平面
平面![]() ;
;
(2)求直线![]() 和平面
和平面![]() 所成角的正弦值;
所成角的正弦值;
(3) 在棱![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的正切值为
所成锐二面角的正切值为![]() ?若存在,指出点
?若存在,指出点![]() 在棱
在棱![]() 上的位置,若不存在,说明理由.
上的位置,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是指大气中直径小于或等于
是指大气中直径小于或等于![]() 微米的颗粒物,也称为可入肺颗粒物,对人体健康和大气环境质量的影响很大.我国
微米的颗粒物,也称为可入肺颗粒物,对人体健康和大气环境质量的影响很大.我国![]() 标准采用世卫组织设定的最宽限值.即
标准采用世卫组织设定的最宽限值.即![]() 日均值在35微克/立方米以下空气质量为一级;在35微克/立方米
日均值在35微克/立方米以下空气质量为一级;在35微克/立方米![]() 75微克/立方米之间空气质量为二级;75微克/立方米以上空气质量为超标.
75微克/立方米之间空气质量为二级;75微克/立方米以上空气质量为超标.
某市环保局从360天的市区![]() 监测数据中统计了1月至10月的每月的平均值(单位:微克/立方米),如下表所示.
监测数据中统计了1月至10月的每月的平均值(单位:微克/立方米),如下表所示.
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 32 | 28 | 25 | 31 | 34 | 33 | 45 | 44 | 63 | 68 |
(1)从5月到10月的这6个数据中任取2个数值,求这个2个数值均为二级的概率;
(2)求月均值![]() 关于月份
关于月份![]() 的回归直线方程
的回归直线方程![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
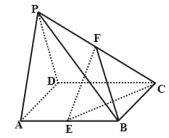
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 是边长为2的正方形,侧面
是边长为2的正方形,侧面![]() 为正三角形,且面
为正三角形,且面![]() 面
面![]() ,
, ![]() 分别为棱
分别为棱![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)(文科)求三棱锥![]() 的体积;
的体积;
(理科)求二面角![]() 的正切值.
的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com