
【题目】在极坐标系中,曲线C的极坐标方程为![]() .以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为
.以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为![]() (t为参数)
(t为参数)
(1)若![]() ,求曲线C的直角坐标方程以及直线l的极坐标方程;
,求曲线C的直角坐标方程以及直线l的极坐标方程;
(2)设点![]() ,曲线C与直线
,曲线C与直线![]() 交于A、B两点,求
交于A、B两点,求![]() 的最小值
的最小值
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为直角梯形![]() ,BC//A
,BC//A![]() ,
,![]() 为正三角形,M为PD中点.
为正三角形,M为PD中点.
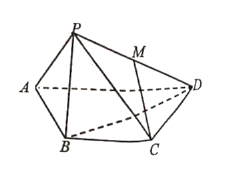
(1)证明:CM//平面PAB;
(2)若二面角P-AB-C的余弦值为![]() ,求直线AD与平面PBD所成角的正弦值.
,求直线AD与平面PBD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数据的收集和整理在当今社会起到了举足轻重的作用,它用统计的方法来帮助人们分析以往的行为习惯,进而指导人们接下来的行动.
某支足球队的主教练打算从预备球员甲、乙两人中选一人为正式球员,他收集到了甲、乙两名球员近期5场比赛的传球成功次数,如下表:
场次 | 第一场 | 第二场 | 第三场 | 第四场 | 第五场 |
甲 | 28 | 33 | 36 | 38 | 45 |
乙 | 39 | 31 | 43 | 39 | 33 |
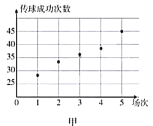
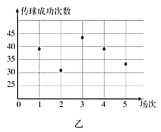
(1)根据这两名球员近期5场比赛的传球成功次数,完成茎叶图(茎表示十位,叶表示个位);分别在平面直角坐标系中画出两名球员的传球成功次数的散点图;
(2)求出甲、乙两名球员近期5场比赛的传球成功次数的平均值和方差;
(3)主教练根据球员每场比赛的传球成功次数分析出球员在场上的积极程度和技术水平,同时根据多场比赛的数据也可以分析出球员的状态和潜力.你认为主教练应选哪位球员?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
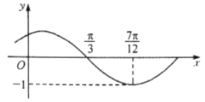
【题目】函数![]() 的图象如图所示,先将函数
的图象如图所示,先将函数![]() 图象上所有点的横坐标变为原来的6倍,纵坐标不变,再将所得函数的图象向左平移
图象上所有点的横坐标变为原来的6倍,纵坐标不变,再将所得函数的图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,下列结论正确的是( )
的图象,下列结论正确的是( )
A.函数![]() 是奇函数B.函数
是奇函数B.函数![]() 在区间
在区间![]() 上是增函数
上是增函数
C.函数![]() 图象关于
图象关于![]() 对称D.函数
对称D.函数![]() 图象关于直线
图象关于直线![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)设函数![]() ,试判断函数
,试判断函数![]() 是否存在最小值,若存在,求出最小值,若不存在,请说明理由.
是否存在最小值,若存在,求出最小值,若不存在,请说明理由.
(Ⅲ)当![]() 时,写出
时,写出![]() 与
与![]() 的大小关系.
的大小关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年9月24日,阿贝尔奖和菲尔兹奖双料得主、英国著名数学家阿蒂亚爵士宣布自己证明了黎曼猜想,这一事件引起了数学界的震动,在1859年,德国数学家黎曼向科学院提交了题目为《论小于某值的素数个数》的论文并提出了一个命题,也就是著名的黎曼猜想.在此之前,著名数学家欧拉也曾研究过这个问题,并得到小于数字![]() 的素数个数大约可以表示为
的素数个数大约可以表示为![]() 的结论(素数即质数,
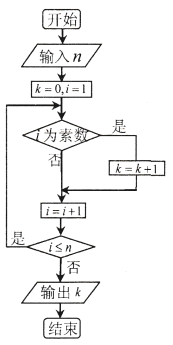
的结论(素数即质数,![]() ).根据欧拉得出的结论,如下流程图中若输入
).根据欧拉得出的结论,如下流程图中若输入![]() 的值为
的值为![]() ,则输出
,则输出![]() 的值应属于区间( )
的值应属于区间( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是椭圆
是椭圆![]() 上一动点,点
上一动点,点![]() 分别是左、右两个焦点.
分别是左、右两个焦点.![]() 面积的最大值为
面积的最大值为![]() ,且椭圆的长轴长为
,且椭圆的长轴长为![]() .
.
(1)求椭圆的标准方程;
(2)若点![]() ,
,![]() 在椭圆上,已知两点
在椭圆上,已知两点![]() ,
,![]() ,且以
,且以![]() 为直径的圆经过坐标原点
为直径的圆经过坐标原点![]() .求证:
.求证:![]() 的面积
的面积![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com