
| OP |
| OA |
| ||
|
|
| ||
|
|
| sinc | ||
|
|
| sinB| | ||
|
|
| AP |
| AD |
|
| ||
| sinC |
|
| ||
| sinB |
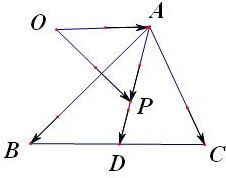 即
即| sinc | ||
|
|
| sinB| | ||
|
|
| sinc | ||
|
|
| sinB| | ||
|
|
| OP |
| OA |
| ||
|
|
| ||
|
|
| OP |
| OA |
| AB |
| AC |
| AB |
| AC |
| AD |
| OP |
| OA |
| AD |
| AP |
| AD |
| AP |
| AD |


科目:高中数学 来源:四川省南山中学2011-2012学年高一下学期期中考试数学试题 题型:013
O为△ABC平面上一定点,该平面上一动点p满足M={P|![]() =
=![]() +λ(
+λ(![]() sinC+
sinC+![]() sinB),λ>0},则△ABC的( )一定属于集合M.
sinB),λ>0},则△ABC的( )一定属于集合M.
A.重心
B.垂心
C.外心
D.内心
查看答案和解析>>
科目:高中数学 来源:山西省康杰中学2011-2012学年高一下学期期中试题数学文科试题 题型:013
设O为△ABC平面上一定点,平面上的动点P满足![]() =
=![]() +λ(
+λ(![]() +
+![]() ),λ∈(0,+∞),则点P轨迹一定通过是△ABC的
),λ∈(0,+∞),则点P轨迹一定通过是△ABC的
A.外心
B.重心
C.内心
D.垂心
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| OP |
| OA |
| ||
|
|
| ||
|
|
| A.重心 | B.垂心 | C.外心 | D.内心 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省绵阳市南山中学高一(下)期中数学试卷(解析版) 题型:选择题
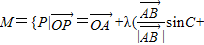
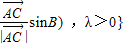 ,则△ABC的( )一定属于集合M.
,则△ABC的( )一定属于集合M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com