
(1)求A与B的值;
(2)证明数列{an}为等差数列;
(3)证明不等式![]() >1对任何正整数m、n都成立.
>1对任何正整数m、n都成立.
思路解析:本题主要考查等差数列的定义、通项公式及利用分析法来证明问题.
(1)解:由已知,得S1=a1=1,S2=a1+a2=7,S3=a1+a2+a3=18.由(5n-8)Sn+1-(5n+2)Sn=An+B,
知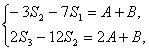
即![]()
解得A=-20,B=-8.
(2)证明:由(1)得(5n-8)Sn+1-(5n+2)Sn=-20n-8. ①
所以(5n-3)Sn+2-(5n+7)Sn+1=-20n-28. ②
②-①得(5n-3)Sn+2-(10n-1)Sn+1+(5n+2)Sn=-20. ③
所以(5n+2)Sn+3-(10n+9)Sn+2+(5n+7)Sn+1=-20. ④
④-③得(5n+2)Sn+3-(15n+6)Sn+2+(15n+6)Sn+1-(5n+2)Sn=0.
因为an+1=Sn+1-Sn,
所以(5n+2)an+3-(10n+4)an+2+(5n+2)an+1=0.
因为(5n+2)≠0,
所以an+3-2an+2+an+1=0.
所以an+3-an+2=an+2-an+1,n≥1.
又a3-a2=a2-a1=5,
所以数列{an}为等差数列.
(3)证明:由(2)可知,an=1+5(n-1)=5n-4,
要证![]() >1,
>1,
只要证5amn>1+aman+![]() .
.
因为amn=5mn-4,aman=(
故只要证5(5mn-4)>1+25mn-20(m+n)+16+![]() ,
,
即只要证![]() ,
,
因为![]() ≤am+an=
≤am+an=
所以原命题得证.


科目:高中数学 来源: 题型:
| 3 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
| 10 |
| 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| Sn |
| 5•2n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com