
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)当点![]() 在椭圆
在椭圆![]() 的图像上运动时,点
的图像上运动时,点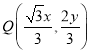 在曲线
在曲线![]() 上运动,求曲线
上运动,求曲线![]() 的轨迹方程,并指出该曲线是什么图形;
的轨迹方程,并指出该曲线是什么图形;
(3)过椭圆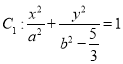 上异于其顶点的任意一点
上异于其顶点的任意一点![]() 作曲线
作曲线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() 不在坐标轴上),若直线
不在坐标轴上),若直线![]() 在
在![]() 轴,
轴,![]() 轴上的截距分别为
轴上的截距分别为![]() 试问:
试问:![]() 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
【答案】(1)![]() (2)
(2)![]() ,曲线
,曲线![]() 的图形是一个以坐标原点为圆心、
的图形是一个以坐标原点为圆心、![]() 为半径的圆 (3)是定值,
为半径的圆 (3)是定值,![]()
【解析】
(1)由![]() 得
得![]() ,再把点
,再把点![]() 坐标代入又得一方程,联立后可解得
坐标代入又得一方程,联立后可解得![]() 得椭圆方程;
得椭圆方程;
(2)设![]() ,用
,用![]() 表示
表示![]() ,把
,把![]() 代入椭圆方程可得曲线
代入椭圆方程可得曲线![]() 方程,由方程可判断曲线形状;
方程,由方程可判断曲线形状;
(3)由(1)知,![]() 设点
设点![]() ,由
,由![]() 坐标可得切线方程,代入
坐标可得切线方程,代入![]() 点坐标于两切线方程后观察结论可得直线
点坐标于两切线方程后观察结论可得直线![]() 方程,求出
方程,求出![]() ,计算
,计算![]() ,利用
,利用![]() 在椭圆
在椭圆![]() 上可得.
上可得.
(1)由题意得,![]() 所以
所以![]()
又点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() 解得
解得![]()
所以椭圆![]() 的标准方程为
的标准方程为![]()
(2)设![]() ,则
,则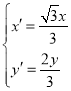 ,于是
,于是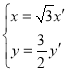 ,
,
由于点![]() 在椭圆
在椭圆![]() 的图像上,
的图像上,
所以 ![]() 即
即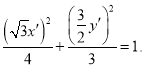
整理得![]() ,
,
所以曲线![]() 的轨迹方程为
的轨迹方程为![]()
曲线![]() 的图形是一个以坐标原点为圆心,
的图形是一个以坐标原点为圆心,![]() 为半径的圆.
为半径的圆.
(3)由(1)知,![]() 设点
设点![]()
则直线![]() 的方程为
的方程为![]() ①
①
直线![]() 的方程为
的方程为![]() ②
②
把点![]() 的坐标代入①②得
的坐标代入①②得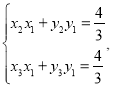
所以直线![]() 的方程为
的方程为![]()
令![]() 得
得![]() 令
令![]() 得
得![]()
所以![]() 又点
又点![]() 在椭圆
在椭圆![]() 上,
上,
所以![]() 即
即![]() 为定值.
为定值.


科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知圆![]() ,圆
,圆![]() ,动圆
,动圆![]() 与圆
与圆![]() 外切并且与圆
外切并且与圆![]() 内切,圆心
内切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)![]() 是与圆
是与圆![]() ,圆
,圆![]() 都相切的一条直线,
都相切的一条直线,![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,当圆
两点,当圆![]() 的半径最长时,求
的半径最长时,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在实数集![]() 上的偶函数
上的偶函数![]() 和奇函数
和奇函数![]() 满足
满足![]() .
.
(1)求![]() 与
与![]() 的解析式;
的解析式;
(2)求证:![]() 在区间
在区间![]() 上单调递增;并求
上单调递增;并求![]() 在区间
在区间![]() 的反函数;
的反函数;
(3)设![]() (其中
(其中![]() 为常数),若
为常数),若![]() 对于
对于![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 中,
中,![]() ,前
,前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)证明:数列![]() 是等差数列,并写出其通项公式;
是等差数列,并写出其通项公式;
(3)设![]() (
(![]() ),试问是否存在正整数
),试问是否存在正整数![]() ,
,![]() (其中
(其中![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等比数列?若存在,求出所有满足条件的数对
成等比数列?若存在,求出所有满足条件的数对![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在
是定义在![]() 上的函数,满足
上的函数,满足 .
.
(1)证明:2是函数![]() 的周期;
的周期;
(2)当![]() 时,
时,![]() ,求
,求![]() 在
在![]() 时的解析式,并写出
时的解析式,并写出![]() 在
在![]() (
(![]() )时的解析式;
)时的解析式;
(3)对于(2)中的函数![]() ,若关于x的方程
,若关于x的方程![]() 恰好有20个解,求实数a的取值范围.
恰好有20个解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)当点![]() 在椭圆
在椭圆![]() 的图像上运动时,点
的图像上运动时,点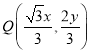 在曲线
在曲线![]() 上运动,求曲线
上运动,求曲线![]() 的轨迹方程,并指出该曲线是什么图形;
的轨迹方程,并指出该曲线是什么图形;
(3)过椭圆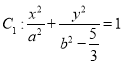 上异于其顶点的任意一点
上异于其顶点的任意一点![]() 作曲线
作曲线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() 不在坐标轴上),若直线
不在坐标轴上),若直线![]() 在
在![]() 轴,
轴,![]() 轴上的截距分别为
轴上的截距分别为![]() 试问:
试问:![]() 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名射击运动员在进行射击训练,已知甲命中10环,9环,8环的概率分别是![]() ,
,![]() ,
,![]() ,乙命中10环,9环,8环的概率分别是
,乙命中10环,9环,8环的概率分别是![]() ,
,![]() ,
,![]() ,任意两次射击相互独立.
,任意两次射击相互独立.
(1)求甲运动员两次射击命中环数之和恰好为18的概率;
(2)现在甲、乙两人进行射击比赛,每一轮比赛两人各射击1次,环数高于对方为胜,环数低于对方为负,环数相等为平局,规定连续胜利两轮的选手为最终的胜者,比赛结束,求恰好进行3轮射击后比赛结束的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com