Question

【题目】在长方体 中， ， ，点 在棱 上移动，则直线 与 所成角的大小是 ， 若 ，则 ．

Answer 1

【答案】90°；1
【解析】长方体ABCD﹣A1B1C1D1中以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，又 ， ，点 在棱 上移动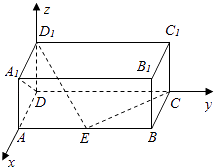

则D（0，0，0），D1（0，0，1），A（1，0，0），A1（1，0，1），C（0，2，0），
设E（1，m，0），0≤m≤2，
则 =（1，m，﹣1）， =（﹣1，0，﹣1），
∴ =﹣1+0+1=0，
∴直线D1E与A1D所成角的大小是90°．
∵ =（1，m，﹣1）， =（﹣1，2﹣m，0），D1E⊥EC，
∴ =﹣1+m（2﹣m）+0=0，
解得m=1，∴AE=1．
故答案为：90°，1．
长方体中的线线角适合建立空间直角坐标系,由直线的方向向量的夹角求线线角.