
 (其中
(其中 ).
). 的单调区间;
的单调区间; 在
在 上有且只有一个零点,求实数
上有且只有一个零点,求实数 的取值范围.
的取值范围.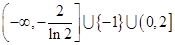 .
. 的定义域与导数
的定义域与导数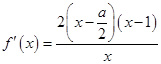 ,对
,对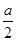 是否在定义域内以及在定义域内与
是否在定义域内以及在定义域内与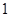 进行大小比较,从而确定函数的单调区间;(2)在(1)的条件下结合函数的单调性与零点存在定理对端点值或极值的正负进行限制,从而求出参数
进行大小比较,从而确定函数的单调区间;(2)在(1)的条件下结合函数的单调性与零点存在定理对端点值或极值的正负进行限制,从而求出参数 的取值范围.
的取值范围.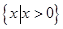 ,
,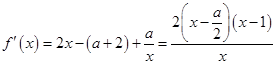 ,
,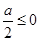 ,即
,即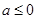 时,
时,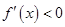 ,得
,得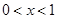 ,函数
,函数 的单调递减区间为
的单调递减区间为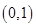 ,
,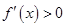 ,得
,得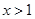 ,函数
,函数 的单调递增区间为
的单调递增区间为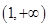 ;
;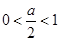 ,即
,即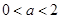 时,
时,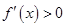 ,得
,得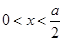 或
或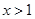 ,函数
,函数 的单调递增区间为
的单调递增区间为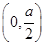 ,
,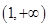 ,
,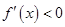 ,得
,得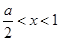 ,函数
,函数 的单调递减区间为
的单调递减区间为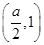 ;
;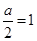 ,即
,即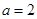 时,
时,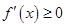 恒成立,函数
恒成立,函数 的单调递增区间为
的单调递增区间为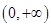 ;
;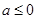 时,由(1)可知,函数
时,由(1)可知,函数 的单调递减区间为
的单调递减区间为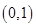 ,
, 在
在 单调递增,
单调递增, 在
在 上的最小值为
上的最小值为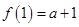 ,
,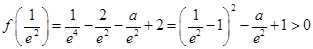 ,
, 在
在 上有且只有一个零点,
上有且只有一个零点,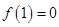 或
或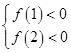 ,解得
,解得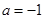 或
或 ,
,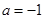 或
或 时,
时, 在
在 上有且只有一个零点;
上有且只有一个零点;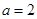 时,由(1)可知,函数
时,由(1)可知,函数 在
在 上单调递增,
上单调递增,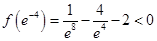 ,
,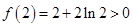 ,
,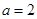 时,
时, 在
在 上有且只有一个零点;
上有且只有一个零点;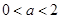 时,由(1)可知,函数
时,由(1)可知,函数 在
在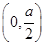 内单调递增,在
内单调递增,在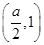 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,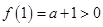 ,所以当
,所以当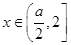 时,总有
时,总有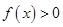 ,
, ,
, ,
, 在区间
在区间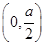 内必有零点,
内必有零点, 在
在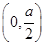 内单调递增,
内单调递增,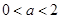 时,
时, 在
在 上有且只有一个零点,
上有且只有一个零点,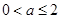 或
或 或
或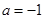 时,
时, 在
在 上有且只有一个零点.
上有且只有一个零点.

科目:高中数学 来源:不详 题型:解答题
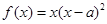 ,
,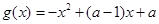 (其中
(其中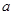 为常数).
为常数).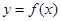 和
和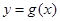 有相同的极值点,求
有相同的极值点,求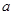 的值;
的值;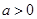 ,问是否存在
,问是否存在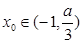 ,使得
,使得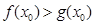 ,若存在,请求出实数
,若存在,请求出实数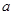 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.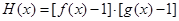 ,若函数
,若函数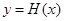 有5个不同的零点,求实数
有5个不同的零点,求实数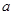 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 .
. 时,求函数
时,求函数 的单调区间;
的单调区间; 在区间
在区间 上为减函数,求实数
上为减函数,求实数 的取值范围;
的取值范围; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com