
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)若函数![]() 有两个不同的零点求a的取值范围.
有两个不同的零点求a的取值范围.
【答案】(1)答案不唯一,具体见解析(2)![]()
【解析】
(1)分类讨论参数![]() 的值,利用导数得出该函数的单调性,进而得出极值;
的值,利用导数得出该函数的单调性,进而得出极值;
(2)当![]() 时,
时,![]() 至多有一个零点,不符合题意;当
至多有一个零点,不符合题意;当![]() 时,函数的极大值为
时,函数的极大值为![]() ,令
,令![]() ,求导确定
,求导确定![]() 的单调性,讨论
的单调性,讨论![]() 的值,确定
的值,确定![]() 的正负,再结合零点存在性定理,即可得出
的正负,再结合零点存在性定理,即可得出![]() 的取值范围.
的取值范围.
解:(1)![]() 的定义域是
的定义域是![]() ,
,![]()
若![]() ,则
,则![]() ,此时
,此时![]() 在
在![]() 递减,无极值;
递减,无极值;
若![]() ,则由
,则由![]() ,解得
,解得![]()
当![]() ,
,![]() ;当
;当![]() 时,
时,![]()
此时![]() 在
在![]() 递增,在
递增,在![]() 递减,
递减,
![]() 当
当![]() 时,函数的极大值为
时,函数的极大值为![]() ,无极小值.
,无极小值.
(2)由(1)可知,当![]() 时,
时,![]() 在
在![]() 递减,则
递减,则![]() 至多有一个零点,不符合题意,舍去;
至多有一个零点,不符合题意,舍去;
当![]() 时,函数的极大值为
时,函数的极大值为![]()
令![]()
![]() ,
,![]() 在
在![]() 单调递增
单调递增
又![]() ,
,![]() 时,
时,![]() ,
,![]() 时,
时,![]()
①当![]() ,
,![]() ,则函数
,则函数![]() 至多有一个零点,不符合题意,舍去;
至多有一个零点,不符合题意,舍去;
②当![]() 时,
时,![]()
![]()
![]() 函数
函数![]() 在
在![]() 内有一个零点
内有一个零点
![]()
设![]()
![]()
![]()
![]() 在
在![]() 内单调递减,则
内单调递减,则![]()
![]() 函数
函数![]() 在
在![]() 内有一个零点,则当
内有一个零点,则当![]() 时,函数
时,函数![]() 恰有两个零点,综上,函数
恰有两个零点,综上,函数![]() 有两个不同的零点时,
有两个不同的零点时,![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】羽毛球比赛中,首局比赛由裁判员采用抛球的方法决定谁先发球,在每回合争夺中,赢方得1分且获得发球权.每一局中,获胜规则如下:①率先得到21分的一方赢得该局比赛;②如果双方得分出现![]() ,需要领先对方2分才算该局获胜;③如果双方得分出现
,需要领先对方2分才算该局获胜;③如果双方得分出现![]() ,先取得30分的一方该局获胜.现甲、乙两名运动员进行对抗赛,在每回合争夺中,若甲发球时,甲得分的概率为
,先取得30分的一方该局获胜.现甲、乙两名运动员进行对抗赛,在每回合争夺中,若甲发球时,甲得分的概率为![]() ;乙发球时,甲得分的概率为
;乙发球时,甲得分的概率为![]() .
.
(Ⅰ)若![]() ,记“甲以
,记“甲以![]() 赢一局”的概率为
赢一局”的概率为![]() ,试比较
,试比较![]() 与
与![]() 的大小;
的大小;
(Ⅱ)根据对以往甲、乙两名运动员的比赛进行数据分析,得到如下![]() 列联表部分数据.若不考虑其它因素对比赛的影响,并以表中两人发球时甲得分的频率作为
列联表部分数据.若不考虑其它因素对比赛的影响,并以表中两人发球时甲得分的频率作为![]() ,
,![]() 的值.
的值.
甲得分 | 乙得分 | 总计 | |
甲发球 | 50 | 100 | |
乙发球 | 60 | 90 | |
总计 | 190 |
①完成![]() 列联表,并判断是否有95%的把握认为“比赛得分与接、发球有关”?
列联表,并判断是否有95%的把握认为“比赛得分与接、发球有关”?
②已知在某局比中,双方战成![]() ,且轮到乙发球,记双方再战
,且轮到乙发球,记双方再战![]() 回合此局比赛结束,求
回合此局比赛结束,求![]() 的分布列与期望.
的分布列与期望.
参考公式: ,其中
,其中![]() .
.
临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,以原点
,以原点![]() 为圆心,椭圆
为圆心,椭圆![]() 的长半轴为半径的圆与直线
的长半轴为半径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知点![]() ,
, ![]() 为动直线
为动直线![]() 与椭圆
与椭圆![]() 的两个交点,问:在
的两个交点,问:在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为定值?若存在,试求出点
为定值?若存在,试求出点![]() 的坐标和定值,若不存在,请说明理由.
的坐标和定值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,CM,CN为某公园景观湖胖的两条木栈道,∠MCN=120°,现拟在两条木栈道的A,B处设置观景台,记BC=a,AC=b,AB=c(单位:百米)
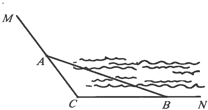
(1)若a,b,c成等差数列,且公差为4,求b的值;
(2)已知AB=12,记∠ABC=θ,试用θ表示观景路线A-C-B的长,并求观景路线A-C-B长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆锥的顶点为S,底面圆O的两条直径分别为AB和CD,且AB⊥CD,若平面![]() 平面
平面![]() .现有以下四个结论:
.现有以下四个结论:
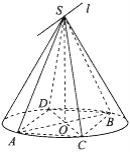
①AD∥平面SBC;
②![]() ;
;
③若E是底面圆周上的动点,则△SAE的最大面积等于△SAB的面积;
④![]() 与平面SCD所成的角为45°.
与平面SCD所成的角为45°.
其中正确结论的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)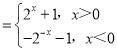 则下列结论错误的是( )
则下列结论错误的是( )
A.函数f(x)的值域为RB.函数f(|x|)为偶函数
C.函数f(x)为奇函数D.函数f(x)是定义域上的单调函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com