
【题目】已知函数![]() 是偶函数.
是偶函数.
(1)求证:![]() 是偶函数;
是偶函数;
(2)求证:![]() 在
在![]() 上是增函数;
上是增函数;
(3)设![]() (
(![]() ,且
,且![]() ),若对任意的
),若对任意的![]() ,在区间
,在区间![]() 上总存在两个不同的数
上总存在两个不同的数![]() ,
,![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】分析:(1)直接利用奇偶性的定义证明即可;(2)设![]() ,则
,则![]()
![]() ,分解因式可得
,分解因式可得![]() ,从而可得结论;(3)由(1)和(2),得
,从而可得结论;(3)由(1)和(2),得![]() 在
在![]() 上是减函数,则
上是减函数,则![]() ,当
,当![]() 时,结合函数图象可得
时,结合函数图象可得 ,解得
,解得![]() ,即
,即![]() ;当
;当![]() 时,直线
时,直线![]() 与函数
与函数![]() 的图象没有交点,不合题意,从而可得结果.
的图象没有交点,不合题意,从而可得结果.
详解:(1)函数![]() 的定义域为
的定义域为![]() ,
,
因为![]() ,
,
所以![]() 是偶函数.
是偶函数.
(2)证明:设![]() ,则
,则![]()
![]()
![]()
![]() .
.
由![]() ,得
,得![]() ,
,![]() ,
,![]() ,
,
所以![]() ,即
,即![]() ,
,
所以![]() 在
在![]() 上是增函数.
上是增函数.
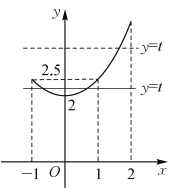
(3)解:由(1)和(2),得![]() 在
在![]() 上是减函数,则
上是减函数,则![]() .
.
![]() .
.
当![]() 时,
时,![]() 的值域为
的值域为![]() .
.
当直线![]() 与函数
与函数![]() 的图象有两个交点时,
的图象有两个交点时,
 ,解得
,解得![]() ,即
,即![]() .
.
当![]() 时,
时,![]() 的值域为
的值域为![]() ,而
,而![]() ,
,
所以直线![]() 与函数
与函数![]() 的图象没有交点,此时不符合题意.
的图象没有交点,此时不符合题意.
综上,所求![]() 的取值范围是
的取值范围是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某几何体的三视图如图所示,且该几何体的体积是3,则正视图的![]() 的值__________.
的值__________.

【答案】3
【解析】 由已知中的三视图可得该几何体是一个以直角梯形为底面,梯形上下边长为![]() 和
和![]() ,高为
,高为![]() ,
,
如图所示, ![]() 平面
平面![]() ,
,
所以底面积为![]() ,
,
几何体的高为![]() ,所以其体积为
,所以其体积为![]() .
.

点睛:在由三视图还原为空间几何体的实际形状时,要从三个视图综合考虑,根据三视图的规则,空间几何体的可见轮廓线在三视图中为实线,不可见轮廓线在三视图中为虚线.在还原空间几何体实际形状时,一般是以正视图和俯视图为主,结合侧视图进行综合考虑.求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系,利用相应体积公式求解.
【题型】填空题
【结束】
16
【题目】已知椭圆![]() :
: ![]() 的右焦点为
的右焦点为![]() ,
, ![]() 为直线
为直线![]() 上一点,线段
上一点,线段![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某百货公司1~6月份的销售量与利润的统计数据如表:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售量x/万件 | 10 | 11 | 13 | 12 | 8 | 6 |
利润y/万元 | 22 | 25 | 29 | 26 | 16 | 12 |
(1)根据2~5月份的统计数据,求出y关于x的回归直线方程![]() x+
x+![]() ;
;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差均不超过2万元,则认为得到的回归直线方程是理想的,试问所得回归直线方程是否理想?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的导函数f′(x)=2+sinx,且f(0)=﹣1,数列{an}是以 ![]() 为公差的等差数列,若f(a2)+f(a3)+f(a4)=3π,则
为公差的等差数列,若f(a2)+f(a3)+f(a4)=3π,则 ![]() =( )
=( )
A.2016
B.2015
C.2014
D.2013
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的短轴长为2,离心率为
的短轴长为2,离心率为![]()
(1)求椭圆C的方程;
(2)设过点M(2,0)的直线l与椭圆C相交于A,B两点,F1为椭圆的左焦点.
①若B点关于x轴的对称点是N,证明:直线AN恒过一定点;
②试求椭圆C上是否存在点P,使F1APB为平行四边形?若存在,求出F1APB的面积,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天气预报说,在今后的三天中,每一天下雨的概率均为![]() ,某同学用随机模拟的方法确定这三天中恰有两天下雨的概率,该同学利用计算器可以产生0到9之间的取整数值的随机数,他用1,4,7表示下雨,用0,2,3,5,6,8,9表示不下雨。实验得出如下20组随机数:
,某同学用随机模拟的方法确定这三天中恰有两天下雨的概率,该同学利用计算器可以产生0到9之间的取整数值的随机数,他用1,4,7表示下雨,用0,2,3,5,6,8,9表示不下雨。实验得出如下20组随机数:
245,368,590,126,217,895,560,061,378,902
542,751,245,602,156,035,682,148,357,438
请根据该同学实验的数据确定这三天中恰有两天下雨的概率为 __________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对函数f(x)= ![]() ,若a,b,c∈R,f(a),f(b),f(c)都为某个三角形的三边长,则实数m的取值范围是( )
,若a,b,c∈R,f(a),f(b),f(c)都为某个三角形的三边长,则实数m的取值范围是( )
A.( ![]() ,6)
,6)
B.( ![]() ,6)
,6)
C.( ![]() ,5)
,5)
D.( ![]() ,5)
,5)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com