
已知函数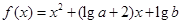 满足
满足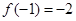 , 且对于任意
, 且对于任意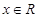 恒有
恒有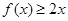 成立。
成立。
(1) 求实数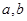 的值;
的值;
(2)设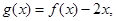 若存在实数
若存在实数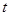 ,当
,当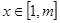 时,
时,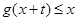 恒成立,求实数
恒成立,求实数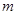 的最大值。
的最大值。
(1)b=10, a=100;(2) 实数 的最大值是4。
的最大值是4。
【解析】(1)由f(-1)=-2,代入函数解析式得到关于lga与lgb的等式记作①,化简后得到关于a与b的等式记作②,又因为f(x)≥2x恒成立,把f(x)的解析式代入后,令△≤0得到关于lga与lgb的不等式,把①代入后得到关于lgb的不等式,根据平方大于等于0,即可求出b的值,把b的值代入②即可求出a的值;
(1)由f(-1)=-2知,lgb-lga+1=0①,所以a b =10②.又f(x)≥2x恒成立,f(x)-2x≥0恒成立,则有x2+x•lga+lgb≥0恒成立,故△=(lga)2-4lgb≤0,将①式代入上式得:(lgb)2-2lgb+1≤0,即(lgb-1)2≤0,故lgb=1即b=10,代入②得,a=100;
(2) 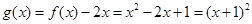 ,∵存在实数
,∵存在实数 ,当
,当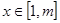 时,
时, 恒成立;即
恒成立;即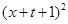
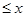 恒成立.
恒成立.
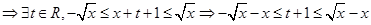 (
(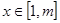 )恒成立.
)恒成立.
设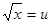 ,则
,则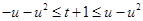
∴ ,即
,即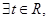
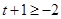 ,且
,且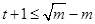
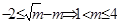 ,∴实数
,∴实数 的最大值是4。
的最大值是4。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知函数![]() 满足
满足![]() ,且
,且![]()
(1)当![]() 时,求
时,求![]() 的表达式;
的表达式;
(2)设![]() ,
,![]() ,求证:
,求证:![]() ;w.w.w.k.s.5.u.c.o.m
;w.w.w.k.s.5.u.c.o.m ![]()
(3)设![]() ,对每一个
,对每一个![]() ,在
,在![]() 与
与![]() 之间插入
之间插入![]() 个
个![]() ,得到新数列
,得到新数列![]() ,设
,设![]() 是数列
是数列![]() 的前
的前![]() 项和,试问是否存在正整数
项和,试问是否存在正整数![]() ,使
,使![]() ?若存在求出
?若存在求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省高三5月模拟考试文科数学试卷(解析版) 题型:选择题
已知函数 满足
满足 ,且
,且 ,若对任意的
,若对任意的 ,
,
总有 成立,则
成立,则 在
在 内的可能值有( )个.
内的可能值有( )个.
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:高中数学 来源:2011年广东省高二第一次阶段性测试题文科数学 题型:解答题
(本小题满分14分)已知函数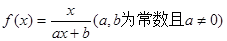 满足
满足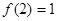 ,且
,且 有唯一实数解。
有唯一实数解。
(1)求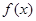 的表达式 ;
的表达式 ;
(2)记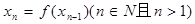 ,且
,且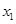 =
=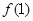 ,求数列
,求数列 的通项公式。
的通项公式。
(3)记 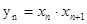 ,数列{
,数列{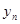 }的前
}的前 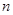 项和为
项和为
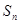 ,是否存在k∈N*,使得
,是否存在k∈N*,使得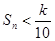 对任意n∈N*恒成立?若存在,求出k的最小值,若不存在,请说明理由.
对任意n∈N*恒成立?若存在,求出k的最小值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013届度广东省高二理科数学月考试卷 题型:解答题
已知函数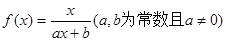 满足
满足 ,且
,且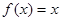 有唯
有唯
一实数解。
(1)求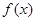 的表达式 ;
的表达式 ;
(2)记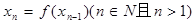 ,且
,且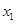 =
=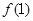 ,求数列
,求数列 的通项公式。
的通项公式。
(3)记 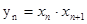 ,数列{
,数列{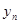 }的前
}的前 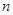 项和为
项和为
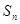 ,是否存在k∈N*,使得
,是否存在k∈N*,使得
对任意n∈N*恒成立?若存在,求出k的最小值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com