练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某地区发现某污染源，相关部门对污染情况进行调查研究后，发现一天中污染指数与时刻x（时）的函数关系为，其中a是与气象有关的参数，且．按规定，若每天污染指数不超过2，则环保合格，否则需要整改．如果以每天中的最大值作为当天的污染指数，并记为，那么该地区污染指数的超标情况为________．

    【答案】当时超标，当时不超标．

    【解析】

    根据题目中已知自变量的取值范围求解参数的取值范围，根据参数的范围得到分段函数的表达式以及定义域上的单调性，由题知的最大值即为，令即可求得不超标时的取值范围，同理可得到超标时的取值范围.

    设，则

    当时，，当时，，所以

    所以

    因为在上单调递减，在上单调递增

    且

    所以即

    当时，；

    当时，；当时，．

    综上，当时超标，当时不超标．

    故答案为：当时超标，当时不超标．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆上任意一点到两焦点距离之和为，离心率为．

    （Ⅰ）求椭圆的标准方程；

    （Ⅱ）若直线的斜率为，直线与椭圆交于两点．点为椭圆上一点，求的面积的最大值及此时直线的直线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数（其中）的部分图象如图所示，把函数的图像向右平移个单位长度，再向下平移1个单位，得到函数的图像.

    （1）当时，求的值域

    （2）令，若对任意都有恒成立，求的最大值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（12分）

    已知函数（a为实数）.

    （1）当时，求函数的图像在处的切线方程；

    （2）求在区间上的最小值；

    （3）若存在两个不等实数，使方程成立，求实数a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】三角形的勃劳卡德点是以法国军官亨利·勃劳卡德（Henri.Brocard）命名的，他在1875年曾描述过这一事实，即：对任何一个三角形都存在唯一的角，即勃劳卡德角，使得图中连接三个顶点的线相交于勃劳卡德点Q，如图所示.

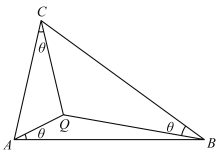
    （1）研究发现：等腰直角三角形中，若是斜边的等腰直角三角形，求线段的长度；

    （2）若中，，，，求的值；

    （3）若中，若线段，，的长度是1为首项，公比为q（）的等比数列，当时，求公比q的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某租赁公司拥有汽车100辆.当每辆车的月租金为元时，可全部租出.当每辆车的月租金每增加50元时，未租出的车将会增加一辆.租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元.若使租赁公司的月收益最大，每辆车的月租金应该定为__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，，若有最小值，则实数的取值范围是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】城镇化是国家现代化的重要指标，据有关资料显示，1978—2013年，我国城镇常住人口从1.7亿增加到7.3亿．假设每一年城镇常住人口的增加量都相等，记1978年后第t（限定）年的城镇常住人口为亿．写出的解析式，并由此估算出我国2017年的城镇常住人口数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，曲线C1的参数方程为(为参数)，曲线C2的参数方程为(为参数)．在以O为极点，x轴的正半轴为极轴的极坐标系中，射线l：θ＝α 与C1，C2 各有一个交点．当 α＝0时，这两个交点间的距离为2，当 α＝时，这两个交点重合．

    (1) 求曲线C1，C2的直角坐标方程

    (2) 设当 α＝时，l与C1，C2的交点分别为A1，B1，当 α＝－时，l与C1，C2的交点分别为A2，B2，求四边形A1A2B2B1的面积．

    查看答案和解析>>

    同步练习册答案