
【题目】密云某商场举办春节优惠酬宾赠券活动,购买百元以上单件商品可以使用优惠劵一张,并且每天购物只能用一张优惠券.一名顾客得到三张优惠券,三张优惠券的具体优惠方式如下:
优惠券1:若标价超过50元,则付款时减免标价的10%;
优惠券2:若标价超过100元,则付款时减免20元;
优惠券3:若标价超过100元,则超过100元的部分减免18%.
如果顾客需要先用掉优惠券1,并且使用优惠券1比使用优惠券2、优惠券3减免的都多,那么你建议他购买的商品的标价可以是__________元.
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】我国南宋数学家杨辉所著的《详解九章算术》一书中,用图①的数表列出了一些正整数在三角形中的一种几何排列,俗称“杨辉三角形”,该数表的规律是每行首尾数字均为![]() ,从第三行开始,其余的数字是它“上方”左右两个数字之和。现将杨辉三角形中的奇数换成
,从第三行开始,其余的数字是它“上方”左右两个数字之和。现将杨辉三角形中的奇数换成![]() ,偶数换成
,偶数换成![]() ,得到图②所示的由数字
,得到图②所示的由数字![]() 和
和![]() 组成的三角形数表,由上往下数,记第
组成的三角形数表,由上往下数,记第![]() 行各数字的和为
行各数字的和为![]() ,如
,如![]() ,则
,则![]() ____________
____________
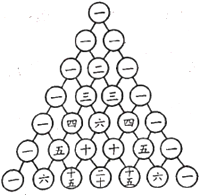

① ②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生活中人们常用“通五经贯六艺”形容一个人才识技艺过人,这里的“六艺”其实源于中国周朝的贵族教育体系,具体包括“礼、乐、射、御、书、数”.为弘扬中国传统文化,某校在周末学生业余兴趣活动中开展了“六艺”知识讲座,每艺安排一节,连排六节,则满足“数”必须排在前两节,“礼”和“乐”必须分开安排的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业质量检验员为了检测生产线上零件的质量情况,从生产线上随机抽取了![]() 个零件进行测量,根据所测量的零件尺寸(单位:mm),得到如下的频率分布直方图:
个零件进行测量,根据所测量的零件尺寸(单位:mm),得到如下的频率分布直方图:

(1)根据频率分布直方图,求这![]() 个零件尺寸的中位数(结果精确到
个零件尺寸的中位数(结果精确到![]() );
);
(2)若从这![]() 个零件中尺寸位于
个零件中尺寸位于![]() 之外的零件中随机抽取
之外的零件中随机抽取![]() 个,设
个,设![]() 表示尺寸在
表示尺寸在![]() 上的零件个数,求
上的零件个数,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(3)已知尺寸在![]() 上的零件为一等品,否则为二等品,将这
上的零件为一等品,否则为二等品,将这![]() 个零件尺寸的样本频率视为概率. 现对生产线上生产的零件进行成箱包装出售,每箱
个零件尺寸的样本频率视为概率. 现对生产线上生产的零件进行成箱包装出售,每箱![]() 个. 企业在交付买家之前需要决策是否对每箱的所有零件进行检验,已知每个零件的检验费用为
个. 企业在交付买家之前需要决策是否对每箱的所有零件进行检验,已知每个零件的检验费用为![]() 元. 若检验,则将检验出的二等品更换为一等品;若不检验,如果有二等品进入买家手中,企业要向买家对每个二等品支付
元. 若检验,则将检验出的二等品更换为一等品;若不检验,如果有二等品进入买家手中,企业要向买家对每个二等品支付![]() 元的赔偿费用. 现对一箱零件随机抽检了
元的赔偿费用. 现对一箱零件随机抽检了![]() 个,结果有
个,结果有![]() 个二等品,以整箱检验费用与赔偿费用之和的期望值作为决策依据,该企业是否对该箱余下的所有零件进行检验?请说明理由.
个二等品,以整箱检验费用与赔偿费用之和的期望值作为决策依据,该企业是否对该箱余下的所有零件进行检验?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数组![]() ,
,![]() ,
,![]()
![]() ,数
,数![]() 称为数组
称为数组![]() 的元素.对于数组
的元素.对于数组![]() ,规定:
,规定:
①数组![]() 中所有元素的和为
中所有元素的和为![]() ;
;
②变换![]() ,
,![]() 将数组
将数组![]() 变换成数组
变换成数组![]() ,其中
,其中![]() 表示不超过
表示不超过![]() 的最大整数;
的最大整数;
③若数组![]() ,则当且仅当
,则当且仅当![]()
![]() 时,
时,![]() .
.
如果对数组![]() 中任意
中任意![]() 个元素,存在一种分法,可将其分为两组,每组
个元素,存在一种分法,可将其分为两组,每组![]() 个元素,使得两组所有元素的和相等,则称数组
个元素,使得两组所有元素的和相等,则称数组![]() 具有性质
具有性质![]() .
.
(Ⅰ)已知数组![]() ,
,![]() ,计算
,计算![]() ,
,![]() ,并写出数组
,并写出数组![]() 是否具有性质
是否具有性质![]() ;
;
(Ⅱ)已知数组![]() 具有性质
具有性质![]() ,证明:
,证明:![]() 也具有性质
也具有性质![]() ;
;
(Ⅲ)证明:数组![]() 具有性质
具有性质![]() 的充要条件是
的充要条件是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四面体![]() 底面的中心为
底面的中心为![]() ,
,![]() 的重心为
的重心为![]() .
.![]() 是
是![]() 内部一动点(包括边界),满足
内部一动点(包括边界),满足![]() ,
,![]() ,
,![]() 不共线且点
不共线且点![]() 到点
到点![]() 的距离与到平面
的距离与到平面![]() 的距离相等.
的距离相等.
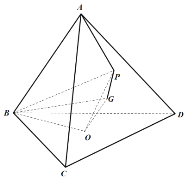
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求四面体
,求四面体![]() 体积的最大值.
体积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市销售某种商品,据统计,该该商品每日的销售量![]() (单位:千克)与销售价格
(单位:千克)与销售价格![]() (单位:元/千克,其中
(单位:元/千克,其中![]() )满足:当
)满足:当![]() 时,
时,![]() (
(![]() ,
,![]() 为常数);当
为常数);当![]() 时,
时,![]() ,已知当销售价格为6元/千克时,每日售出该商品170千克.
,已知当销售价格为6元/千克时,每日售出该商品170千克.
(1)求![]() ,
,![]() 的值,并确定
的值,并确定![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)若该商品的销售成本为3元/千克,试确定销售价格![]() 的值,使店铺每日销售该商品所获利润
的值,使店铺每日销售该商品所获利润![]() 最大.
最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国许多省市雾霾天气频发,为增强市民的环境保护意识,某市面向全市征召![]() 名义务宣传志愿者,成立环境保护宣传组织,现把该组织的成员按年龄分成
名义务宣传志愿者,成立环境保护宣传组织,现把该组织的成员按年龄分成![]() 组第
组第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示,已知第
,得到的频率分布直方图如图所示,已知第![]() 组有
组有![]() 人.
人.

(1)求该组织的人数;
(2)若在第![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 名志愿者参加某社区的宣传活动,应从第
名志愿者参加某社区的宣传活动,应从第![]() 组各抽取多少名志愿者?
组各抽取多少名志愿者?
(3)在(2)的条件下,该组织决定在这![]() 名志愿者中随机抽取
名志愿者中随机抽取![]() 名志愿者介绍宣传经验,求第
名志愿者介绍宣传经验,求第![]() 组至少有
组至少有![]() 名志愿者被抽中的概率.
名志愿者被抽中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com