
【题目】用2与0两个数字排成7位的数码,其中“20”和“02”各至少出现两次(如0020020、2020200、0220220等),则这样的数码的个数是( )
A.54B.44C.32D.22
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,侧面SCD为钝角三角形且垂直于底面ABCD,CD=SD,点M是SA的中点,AD//BC,∠ABC=90°,AB=AD![]() BC=a.
BC=a.
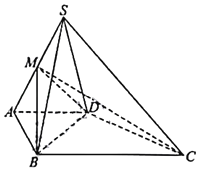
(1)求证:平面MBD⊥平面SCD;
(2)若∠SDC=120°,求三棱锥C﹣MBD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了茎叶图:则下列结论中表述不正确的是
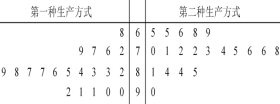
A. 第一种生产方式的工人中,有75%的工人完成生产任务所需要的时间至少80分钟
B. 第二种生产方式比第一种生产方式的效率更高
C. 这40名工人完成任务所需时间的中位数为80
D. 无论哪种生产方式的工人完成生产任务平均所需要的时间都是80分钟.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的普通方程为:
的普通方程为:![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,正方形
,正方形![]() 的顶点都在
的顶点都在![]() 上,且
上,且![]() 逆时针依次排列,点
逆时针依次排列,点![]() 的极坐标为
的极坐标为![]()
(1)写出曲线![]() 的参数方程,及点
的参数方程,及点![]() 的直角坐标;
的直角坐标;
(2)设![]() 为椭圆
为椭圆![]() 上的任意一点,求:
上的任意一点,求:![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表为![]() 年至
年至![]() 年某百货零售企业的线下销售额(单位:万元),其中年份代码
年某百货零售企业的线下销售额(单位:万元),其中年份代码![]() 年份
年份![]() .
.
年份代码 |
|
|
|
|
线下销售额 |
|
|
|
|
(1)已知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测
的线性回归方程,并预测![]() 年该百货零售企业的线下销售额;
年该百货零售企业的线下销售额;
(2)随着网络购物的飞速发展,有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑,某调查平台为了解顾客对该百货零售企业的线下销售额持续增长的看法,随机调查了![]() 位男顾客、
位男顾客、![]() 位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有
位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有![]() 人、女顾客有
人、女顾客有![]() 人,能否在犯错误的概率不超过
人,能否在犯错误的概率不超过![]() 的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
参考公式及数据: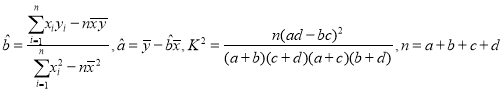 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设点![]() 是抛物线
是抛物线![]() 的焦点,直线
的焦点,直线![]() 与抛物线
与抛物线![]() 相切于点
相切于点![]() (点
(点![]() 位于第一象限),并与抛物线
位于第一象限),并与抛物线![]() 的准线相交于点
的准线相交于点![]() .过点
.过点![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 交抛物线
交抛物线![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,连结
,连结![]() .
.
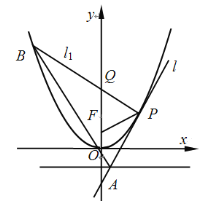
(1)证明:![]() 为等腰三角形;
为等腰三角形;
(2)求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学中有许多寓意美好的曲线,曲线![]() 被称为“四叶玫瑰线”(如图所示).
被称为“四叶玫瑰线”(如图所示).

给出下列三个结论:
①曲线![]() 关于直线
关于直线![]() 对称;
对称;
②曲线![]() 上任意一点到原点的距离都不超过
上任意一点到原点的距离都不超过![]() ;
;
③存在一个以原点为中心、边长为![]() 的正方形,使得曲线
的正方形,使得曲线![]() 在此正方形区域内(含边界).
在此正方形区域内(含边界).
其中,正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了实施“科技下乡,精准脱贫”战略,某县科技特派员带着![]() 三个农业扶贫项目进驻某村,对仅有的四个贫困户进行产业帮扶.经过前期走访得知,这四个贫困户甲、乙、丙、丁选择
三个农业扶贫项目进驻某村,对仅有的四个贫困户进行产业帮扶.经过前期走访得知,这四个贫困户甲、乙、丙、丁选择![]() 三个项目的意向如下:
三个项目的意向如下:
扶贫项目 |
|
|
|
贫困户 | 甲、乙、丙、丁 | 甲、乙、丙 | 丙、丁 |
若每个贫困户只能从自己已登记的选择意向中随机选取一项,且每个项目至多有两个贫困户选择,则甲乙两户选择同一个扶贫项目的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 是正方形,顶点
是正方形,顶点![]() 在底面的射影是底面的中心,且各顶点都在同一球面上,若该四棱锥的侧棱长为
在底面的射影是底面的中心,且各顶点都在同一球面上,若该四棱锥的侧棱长为![]() ,体积为4,且四棱锥的高为整数,则此球的半径等于( )(参考公式:
,体积为4,且四棱锥的高为整数,则此球的半径等于( )(参考公式:![]() )
)
A. 2B. ![]() C. 4D.
C. 4D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com