
我国西部某省4A级风景区内住着一个少数民族村,该村投资了800万元修复和加强民俗文化基础设施,据调查,修复好村民俗文化基础设施后,任何一个月内(每月按30天计算)每天的旅游人数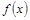 与第x天近似地满足
与第x天近似地满足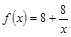 (千人),且参观民俗文化村的游客人均消费
(千人),且参观民俗文化村的游客人均消费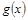 近似地满足
近似地满足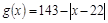 (元).
(元).
(1)求该村的第x天的旅游收入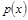 (单位千元,1≤x≤30,
(单位千元,1≤x≤30,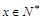 )的函数关系;
)的函数关系;
(2)若以最低日收入的20%作为每一天的计量依据,并以纯收入的5%的税率收回投资成本,试问该村在两年内能否收回全部投资成本?
(1)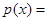
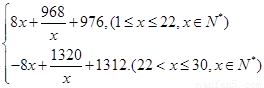 ;(2)能收回投资.
;(2)能收回投资.
【解析】
试题分析:(1)函数应用题关键是找到等量关系,函数关系,不等关系,列出相应的式子就可解题,一般情况下,这些关系式在题中都有提示,但有时我们也要注意生活中的常识,如本题中某天的旅游收入应该等于这天的人均消费乘以这天的旅游人数,即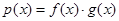 ,此题中
,此题中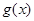 含绝对值符号,我们在求
含绝对值符号,我们在求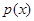 时,可分类讨论,用分段函数形式表示;(2)关键是求
时,可分类讨论,用分段函数形式表示;(2)关键是求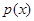 的最小值,如最小值为
的最小值,如最小值为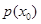 ,我们只要再计算
,我们只要再计算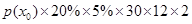 ,如果这个值不小于800万元,就能收回全部投资成本,否则就不能,而
,如果这个值不小于800万元,就能收回全部投资成本,否则就不能,而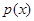 的最小值要分段求,一个用基本不等式,一个用函数的单调性,分别救出后比较,取较小的一个即可.
的最小值要分段求,一个用基本不等式,一个用函数的单调性,分别救出后比较,取较小的一个即可.
试题解析:(1)依据题意,有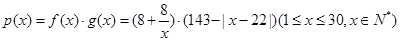
=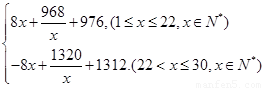
(2) 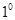 当
当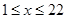 ,
,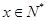 时,
时,
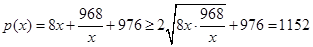 (当且仅当
(当且仅当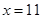 时,等号成立) .
时,等号成立) .
因此,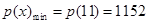 (千元) .
(千元) .
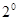 当
当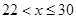 ,
,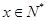 时,
时,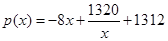 .
.
考察函数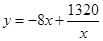 的图像,可知
的图像,可知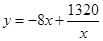 在
在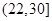 上单调递减,
上单调递减,
于是,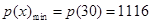 (千元) .
(千元) .
又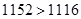 ,
,
所以,日最低收入为1116千元.
该村两年可收回的投资资金为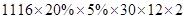 =8035.2(千元)=803.52(万元) .
=8035.2(千元)=803.52(万元) .
因803.52万元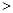 800万元,
800万元,
所以,该村两年内能收回全部投资资金.
考点:(1)分段函数解析式;(2)分段函数的最值问题.


科目:高中数学 来源: 题型:
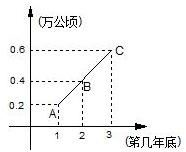 全世界每年都有大量土地被沙漠吞没,保护土地资源,已成为一项十分紧迫的任务.据统计,在我国西部地区,1998年共有沙漠面积100万公顷,1999年至2002年三年的沙漠面积变化情况如图所示(图中横轴数字表示时间,1,2,3分别表示第1,2,3年年底;纵轴数字表示相应时间对应的沙漠面积比原有面积的增加数;A,B,C三点在一条直线上).经过专家考察预测,该地区的沙漠面积若干年内将继续按此规律扩大.若以1999年为第1年进行计算,
全世界每年都有大量土地被沙漠吞没,保护土地资源,已成为一项十分紧迫的任务.据统计,在我国西部地区,1998年共有沙漠面积100万公顷,1999年至2002年三年的沙漠面积变化情况如图所示(图中横轴数字表示时间,1,2,3分别表示第1,2,3年年底;纵轴数字表示相应时间对应的沙漠面积比原有面积的增加数;A,B,C三点在一条直线上).经过专家考察预测,该地区的沙漠面积若干年内将继续按此规律扩大.若以1999年为第1年进行计算,查看答案和解析>>
科目:高中数学 来源: 题型:
| 年降水量(mm) | [100,150 ) | [150,200 ) | [200,250 ) | [250,300] |
| 概 率 | 0.21 | 0.16 | 0.13 | 0.12 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 8 | x |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年上海黄浦区高三上学期期末考试(即一模)理数学卷(解析版) 题型:解答题
我国西部某省4A级风景区内住着一个少数民族村,该村投资了800万元修复和加强民俗文化基础设施,据调查,修复好村民俗文化基础设施后,任何一个月内(每月按30天计算)每天的旅游人数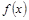 与第x天近似地满足
与第x天近似地满足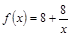 (千人),且参观民俗文化村的游客人均消费
(千人),且参观民俗文化村的游客人均消费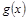 近似地满足
近似地满足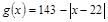 (元).
(元).
(1)求该村的第x天的旅游收入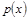 (单位千元,1≤x≤30,
(单位千元,1≤x≤30,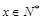 )的函数关系;
)的函数关系;
(2)若以最低日收入的20%作为每一天的计量依据,并以纯收入的5%的税率收回投资成本,试问该村在两年内能否收回全部投资成本?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com