
【题目】解关于x的不等式:(a+1)x2-(2a+3)x+2<0.
【答案】答案见解析。
【解析】
因为二次项系数a+1含字母,应对a+1分等于0、大于0、小于0三种情况讨论。当a+1=0时,不等式转化为一次不等式;当a+1大于0、小于0时,结合二次函数图像解一元二次不等式即可。
(1)当a+1=0即 a=-1时,原不等式变为-x+2<0, 即x>2.
(2)当a+1>0即a>-1时,原不等式可转化为![]()
方程![]() 的根是
的根是![]() 。
。
若-1<a<![]() ,则
,则![]() >2,解得2<x<
>2,解得2<x<![]() ;
;
若a=![]() ,则
,则![]() =2,解得x∈;
=2,解得x∈;
若a>![]() ,则
,则![]() <2, 解得
<2, 解得![]() <x<2.
<x<2.
(3)当a<-1时,原不等式可转化为![]() .
.
∵a<-1,∴![]() <2, 解得x<
<2, 解得x<![]() 或x>2.
或x>2.
综上可知,
当a>![]() 时,原不等式的解集为{x|
时,原不等式的解集为{x|![]() <x<2};
<x<2};
当a=![]() 时,原不等式的解集为;
时,原不等式的解集为;
当-1<a<![]() 时,原不等式的解集为{x|2<x<
时,原不等式的解集为{x|2<x<![]() }.
}.
当a=-1时,原不等式的解集为{x|x>2}.
当a<-1时,原不等式的解集为{x| x<![]() 或x>2}.
或x>2}.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】关于异面直线![]() ,有下列四个命题:
,有下列四个命题:
(1)过直线![]() 有且仅有一个平面
有且仅有一个平面![]() ,使
,使![]() //
//![]() ;
;
(2)过直线![]() 有且仅有一个平面
有且仅有一个平面![]() ,使
,使![]()
![]()
![]() ;
;
(3)在空间中存在平面![]() ,使
,使![]() //
//![]() ,
,![]() //
//![]() ;
;
(4)在空间中不存在平面![]() ,使
,使![]()
![]()
![]() ,
,![]()
![]()
![]() ;
;
其中正确命题的序号是____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面上,我们如果用一条直线去截正方形的一个角,那么截下的一个直角三角形,按图所标边长,由勾股定理有:c2=a2+b2。设想正方形换成正方体,把截线换成如下图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O![]() LMN,如果用S1,S2,S3表示三个侧面面积,S4表示截面面积,那么你类比得到的结论是 .
LMN,如果用S1,S2,S3表示三个侧面面积,S4表示截面面积,那么你类比得到的结论是 .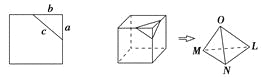
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区为了解辖区住户中离退休老人每天的平均户外“活动时间”,从辖区住户的离退休老人中随机抽取了100位老人进行调查,获得了每人每天的平均户外“活动时间”(单位:小时),活动时间按照[0,0.5),[0.5,1),…,[4,4.5]从少到多分成9组,制成样本的频率分布直方图如图所示.

(Ⅰ)求图中a的值;
(Ⅱ)估计该社区住户中离退休老人每天的平均户外“活动时间”的中位数;
(III)在[1.5,2)、[2,2.5)这两组中采用分层抽样抽取9人,再从这9人中随机抽取2人,求抽取的两人恰好都在同一个组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 是等腰三角形,且
是等腰三角形,且![]() .四边形
.四边形![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)当平面![]()
![]() 平面
平面![]() 时,求四棱锥
时,求四棱锥![]() 的体积;
的体积;
(Ⅲ)请在图中所给的五个点![]() 中找出两个点,使得这两点所在的直线与直线
中找出两个点,使得这两点所在的直线与直线![]() 垂直,并给出证明.
垂直,并给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)在区间A上,对a,b,c∈A,f(a),f(b),f(c)为一个三角形的三边长,则称函数f(x)为“三角形函数”.已知函数f(x)=xlnx+m在区间[ ![]() ,e]上是“三角形函数”,则实数m的取值范围为( )
,e]上是“三角形函数”,则实数m的取值范围为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com