
【题目】已知函数![]() (其中
(其中![]() 是自然对数的底数),
是自然对数的底数),![]() ,
,![]() .
.
(1)记函数![]() ,且
,且![]() ,求
,求![]() 的单调增区间;
的单调增区间;
(2)若对任意![]() ,
,![]() ,
,![]() ,均有
,均有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】试题分析:(1)求单调区间的方法是求出![]() 的解
的解![]() ,确定
,确定![]() (或
(或![]() )的取值区间,即函数的单调区间,此可用列表方法得出(同时可得出极值);(2)本小题不等式
)的取值区间,即函数的单调区间,此可用列表方法得出(同时可得出极值);(2)本小题不等式![]() 或有绝对值符号,有两个参数
或有绝对值符号,有两个参数![]() ,由于函数
,由于函数![]() 是增函数,因此设
是增函数,因此设![]() ,则有
,则有![]() ,原问题等价于
,原问题等价于![]() 恒成立,
恒成立,
分两个问题,![]() 恒成立和
恒成立和![]() 恒成立,前面转化为
恒成立,前面转化为![]() ,可以考虑函数
,可以考虑函数![]() 在
在![]() 上是单调递增的,后面一个转化为
上是单调递增的,后面一个转化为![]() ,可以考虑函数
,可以考虑函数![]() 在
在![]() 上是单调递增的.
上是单调递增的.
试题解析:(1)![]() ,
,![]() ,
,
得![]() 或
或![]() ,
,
列表如下:(![]() ,
,![]() )
)
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极大值 |
| 极小值 |
|
![]() 的单调增区间为:
的单调增区间为:![]() ,
,![]() ,减区间为
,减区间为![]() ;
;
(2)设![]() ,
,![]() 是单调增函数,
是单调增函数,![]() ,
,
![]() ;
;
①由![]() 得:
得:![]() ,
,
即函数![]() 在
在![]() 上单调递增,
上单调递增,
![]() 在
在![]() 上恒成立,
上恒成立,
![]() 在
在![]() 上恒成立;
上恒成立;
令![]() ,
,![]() ,
,
![]()
![]() 时,
时,![]() ;
;![]() 时,
时,![]() ;
;
![]() ,
,
![]() ;
;
②由![]() 得:
得:![]() ,
,
即函数![]() 在
在![]() 上单调递增,
上单调递增,
![]() 在
在![]() 上恒成立,
上恒成立,
![]() 在
在![]() 上恒成立;
上恒成立;
![]() 函数
函数![]() 在
在![]() 上单调递减,
上单调递减,![]() 当
当![]() 时,
时,![]() ,
,
![]() ,
,
综上所述,实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知F1,F2分别为双曲线![]() 的左、右焦点,P为双曲线右支上的任意一点,若
的左、右焦点,P为双曲线右支上的任意一点,若![]() 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )
A. (1,+∞) B. (1,2] C. (1,![]() ] D. (1,3]
] D. (1,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】宝宝的健康成长是妈妈们最关心的问题,父母亲为婴儿选择什么品牌的奶粉一直以来都是育婴中的一个重要话题,为了解过程奶粉的知名度和消费者的信任度,某调查小组特别调查记录了某大型连锁超市2015年与2016年这两年销售量前5名的五个品牌奶粉的销量(单位:罐),绘制如下的管状图:
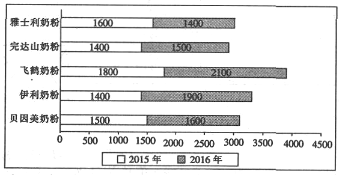
(1)根据给出的这两年销量的管状图,对该超市这两年品牌奶粉销量的前五强进行排名;
(2)分别计算这5个品牌奶粉2016年所占总销量(仅指这5个品牌奶粉的总销量)的百分比(百分数精确到各位),并将数据填入如下饼状图中的括号内;
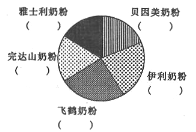
(3)试以(2)中的百分比作为概率,若随机选取2名购买这5个品牌中任意1个品牌的消费者进行采访,记![]() 为被采访中购买飞鹤奶粉的人数,求
为被采访中购买飞鹤奶粉的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2x﹣cosx,{an}是公差为 ![]() 的等差数列,f(a1)+f(a2)+…+f(a5)=5π,则[f(a3)]2﹣a1a5=( )
的等差数列,f(a1)+f(a2)+…+f(a5)=5π,则[f(a3)]2﹣a1a5=( )
A.0
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱台![]() 中,
中, ![]() 与
与![]() 分别是棱长为1与2的正三角形,平面
分别是棱长为1与2的正三角形,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点,
中点, ![]() (
(![]() ,
, ![]() ).
).

(1)设![]() 中点为
中点为![]() ,
, ![]() ,求证:
,求证: ![]() 平面
平面![]() ;
;
(2)若![]() 到平面
到平面![]() 的距离为
的距离为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为 (
(![]() 为参数)以
为参数)以![]() 轴为极轴,
轴为极轴, ![]() 为极点建立极坐标系,在该极坐标系下,圆
为极点建立极坐标系,在该极坐标系下,圆![]() 是以点
是以点![]() 为圆心,且过点
为圆心,且过点![]() 的圆心.
的圆心.
(1)求圆![]() 及圆
及圆![]() 在平而直角坐标系
在平而直角坐标系![]() 下的直角坐标方程;
下的直角坐标方程;
(2)求圆![]() 上任一点
上任一点![]() 与圆
与圆![]() 上任一点之间距离的最小值.
上任一点之间距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4 坐标系与参数方程
在直角坐标系![]() 中,圆
中,圆![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() 为参数),并以
为参数),并以![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)写出![]() 的极坐标方程,并将
的极坐标方程,并将![]() 化为普通方程;
化为普通方程;
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() 与
与![]() 相交于
相交于![]() 两点,
两点,
求![]() 的面积(
的面积(![]() 为圆
为圆![]() 的圆心).
的圆心).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,离心率
轴上,离心率![]() .以两个焦点和短轴的两个端点为顶点的四边形的周长为8,面积为
.以两个焦点和短轴的两个端点为顶点的四边形的周长为8,面积为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若点![]() 为椭圆
为椭圆![]() 上一点,直线
上一点,直线![]() 的方程为
的方程为![]() ,求证:直线
,求证:直线![]() 与椭圆
与椭圆![]() 有且只有一个交点.
有且只有一个交点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com