
已知函数f(x)=(1+x)2-4a lnx(a∈N﹡).
(Ⅰ)若函数f(x)在(1,+∞)上是增函数,求a的值;
(Ⅱ)在(Ⅰ)的条件下,若关于x的方程f(x)=x2-x+b在区间[1,e]上恰有一个实根,求实数b的取值范围.
⑴ ;⑵
;⑵ 或
或 为所求.
为所求.
【解析】
试题分析:⑴由题意,函数 的定义域为
的定义域为
由
知 对
对 恒成立,记
恒成立,记
由于函数 在
在 上是增函数,故
上是增函数,故 ,所以
,所以
又 ,所以
,所以 为所求.
5分
为所求.
5分
⑵由题知 ,整理得
,整理得
记 ,则
,则
注意到 ,故函数
,故函数 在
在 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.
由 知,
知,
所以关于 的方程
的方程 在区间
在区间 上恰有一个实根 时
上恰有一个实根 时
 或
或 为所求.
为所求.
考点:本题考查了导数的运用
点评:近几年新课标高考对于函数与导数这一综合问题的命制,一般以有理函数与半超越(指数、对数)函数的组合复合且含有参量的函数为背景载体,解题时要注意对数式对函数定义域的隐蔽,这类问题重点考查函数单调性、导数运算、不等式方程的求解等基本知识,注重数学思想(分类与整合、数与形的结合)方法(分析法、综合法、反证法)的运用.把数学运算的“力量”与数学思维的“技巧”完美结合


科目:高中数学 来源: 题型:
(08年上虞市质检一文) 已知函数f(x)=ax4+bx2+c的图象经过点(0,2),且在x=1处的切线方程
是y=-4x+![]() .
.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)求函数y=f(x)在区间[-4,1]上的最值.查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南省原名校高三上学期期联考文科数学试卷(解析版) 题型:解答题
已知函数f(x)=2sin(ωx+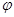 )(ω>0,0<
)(ω>0,0<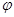 <π)的图象如图所示.
<π)的图象如图所示.

(1)求函数f(x)的解析式:
(2)已知 =
= ,且a∈(0,
,且a∈(0, ),求f(a)的值.
),求f(a)的值.
查看答案和解析>>
科目:高中数学 来源:2014届河南省原名校联盟高三上学期第一次摸底考试理科数学试卷(解析版) 题型:解答题
已知函数f(x)=ln -a
-a +x(a>0).
+x(a>0).
(Ⅰ)若 =
= ,求f(x)图像在x=1处的切线的方程;
,求f(x)图像在x=1处的切线的方程;
(Ⅱ)若 的极大值和极小值分别为m,n,证明:
的极大值和极小值分别为m,n,证明: .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年高三一轮精品复习单元测试(12)数学试卷解析版 题型:解答题
(本小题满分12分)已知函数f(x)=x3+ax2+bx+c在x=-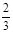 与x=1时都取得极值.
与x=1时都取得极值.
(1)求a、b的值与函数f(x)的单调区间;
(2)xÎ〔-1,2〕,不等式f(x)<c2恒成立,求c的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com