
如图,在三棱锥V-ABC中,已知∠VAB=∠VAC=∠ABC= ,且BC=a,AB=b,AV=c,求:
,且BC=a,AB=b,AV=c,求:

(1)二面角A-VB-C的平面角的度数;
(2)BV与CA夹角的余弦值.
|
解法1:(1)∵VA⊥AB,VA⊥AC,∴VA⊥平面ABC ∴BC⊥VA,又∵BC⊥AB, ∴平面VBC⊥平面VAB ∴二面角A-VB-C的平面角为 (2)作 ∴BV与CA的夹角为∠ ∵ ∴ 解法2:以B为原点, (1)∵ 又∵BC⊥AB ∴BC⊥平面VAB ∴平面VBC⊥平面VAB ∴二面角A-VB-C的平面角为 (2)cos〈 分析 (1)由BC⊥AB,应用线面垂直、面面垂直的判定定理可证明平面ABC⊥平面VAB. (2)异面直线所成的角需要选择一个点,然后引平行线,做出所成的角. |
|
本题还可用建立坐标系求解,即以C为原点,CA、CB、 |


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ(0<θ<
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ(0<θ<| π |
| 2 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ(0<θ<
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ(0<θ<| π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在三棱锥V-ABC中,VA⊥平面ABC,∠ABC=90°,且AC=2BC=2VA=4.
如图,在三棱锥V-ABC中,VA⊥平面ABC,∠ABC=90°,且AC=2BC=2VA=4.查看答案和解析>>
科目:高中数学 来源: 题型:
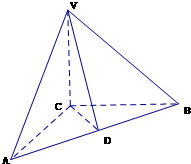 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=45°.
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=45°.查看答案和解析>>
科目:高中数学 来源:2007年湖北省高考数学试卷(理科)(解析版) 题型:解答题
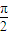 ).
).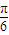 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com