
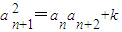 (k为常数).
(k为常数).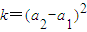 ,求证:a1,a2,a3成等差数列;
,求证:a1,a2,a3成等差数列;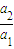 的值;
的值;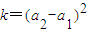 ,代入
,代入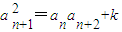 ,令n=1化简即可证明;
,令n=1化简即可证明;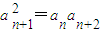 ,由于数列{an}的各项都为正数,可得数列{an}是等比数列,设公比为q>0,根据a2,a4,a5成等差数列,可得a2+a5=2a4,即
,由于数列{an}的各项都为正数,可得数列{an}是等比数列,设公比为q>0,根据a2,a4,a5成等差数列,可得a2+a5=2a4,即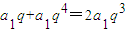 ,解出即可;
,解出即可; ,使得an+an+2=λan+1对任意n∈N*都成立.由
,使得an+an+2=λan+1对任意n∈N*都成立.由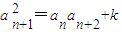 ,及
,及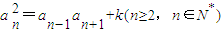 ,可得
,可得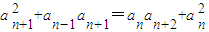 ,由于an>0,两边同除以anan+1,得到
,由于an>0,两边同除以anan+1,得到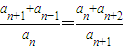 ,进而
,进而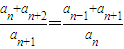 =…=
=…=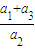 ,即当n∈N*时,都有
,即当n∈N*时,都有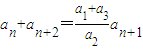 ,再利用已知求出a1,a2,a3即可证明.
,再利用已知求出a1,a2,a3即可证明.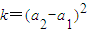 ,
,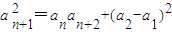 ,
,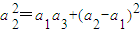 ,
,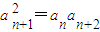 ,
,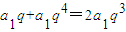 ,
,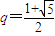 .
.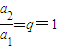 或
或 .
.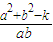 ,使得an+an+2=λan+1对任意n∈N*都成立.
,使得an+an+2=λan+1对任意n∈N*都成立.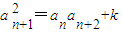 ,∴
,∴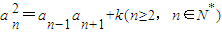 ,
, ,即
,即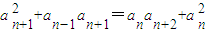 ,
,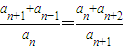 ,
,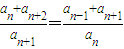 =…=
=…=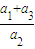 ,
,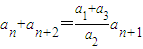 ,
,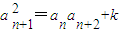 ,
, .∴
.∴ =
= .
.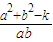 ,使得an+an+2=λan+1对任意n∈N*都成立.
,使得an+an+2=λan+1对任意n∈N*都成立.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| 2n |
| 3n+1 |
| 3 |
| 5 |
| 11 |
| 17 |
查看答案和解析>>
科目:高中数学 来源:江西省赣县中学2011届高三适应性考试数学理科试题 题型:013
已知数列{an}的通项为an=3n+8,下列各选项中的数为数列{an}中的项的是
8
16
32
36
查看答案和解析>>
科目:高中数学 来源:2011年高三数学复习(第6章 数列):6.1 数列定义与通项(解析版) 题型:解答题
 ,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1)
,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1) (2)
(2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com