
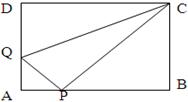
(12分) 如图正方形 的边长为
的边长为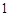 ,
,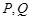 分别为边
分别为边 上的点,当
上的点,当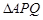 的周长为
的周长为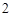 时,求
时,求 的大小.
的大小.
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案科目:高中数学 来源: 题型:
(本小题满分12分)
如图,已知两个正方行ABCD 和DCEF不在同一平面内,M,N分别为AB,DF的中点 。
(I)若平面ABCD ⊥平面DCEF,求直线MN与平面DCEF所成角的正值弦;
(II)用反证法证明:直线ME 与 BN 是两条异面直线。 ![]()
![]()

查看答案和解析>>
科目:高中数学 来源:2014届福建省高一下学期期末数学试卷(解析版) 题型:解答题
(本小题满分12分)如图,定点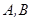 的坐标分别为
的坐标分别为 ,一质点
,一质点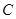 从原点出发,始终沿
从原点出发,始终沿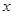 轴的正方向运动,已知第1分钟内,质点
轴的正方向运动,已知第1分钟内,质点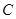 运动了1个单位,之后每分钟内比上一分钟内多运动了2个单位,记第
运动了1个单位,之后每分钟内比上一分钟内多运动了2个单位,记第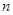 分钟内质点运动了
分钟内质点运动了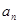 个单位,此时质点的位置为
个单位,此时质点的位置为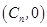 .
.

(Ⅰ)求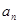 、
、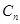 的表达式;
的表达式;
(Ⅱ)当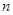 为何值时,
为何值时,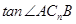 取得最大,最大值为多少?
取得最大,最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
(2009辽宁卷理)(本小题满分12分)
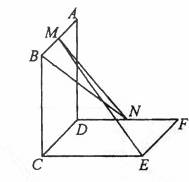
如图,已知两个正方行ABCD 和DCEF不在同一平面内,M,N分别为AB,DF的中点 。
(I)若平面ABCD ⊥平面DCEF,求直线MN与平面DCEF所成角的正值弦;
(II)用反证法证明:直线ME 与 BN 是两条异面直线。
查看答案和解析>>
科目:高中数学 来源: 题型:
(2009辽宁卷理)(本小题满分12分)
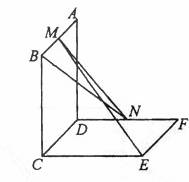
如图,已知两个正方行ABCD 和DCEF不在同一平面内,M,N分别为AB,DF的中点 。
(I)若平面ABCD ⊥平面DCEF,求直线MN与平面DCEF所成角的正值弦;
(II)用反证法证明:直线ME 与 BN 是两条异面直线。
查看答案和解析>>
科目:高中数学 来源: 题型:
(2012年高考上海卷理科21)(6+8=14分)海事救援船对一艘失事船进行定位:以失事船的当前位置为原点,以正北方向为![]() 轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里
轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里![]() 处,如图.现假设:①失事船的移动路径可视为抛物线
处,如图.现假设:①失事船的移动路径可视为抛物线![]() ;②定位后救援船即刻沿直线匀速前往救援;③救援船出发
;②定位后救援船即刻沿直线匀速前往救援;③救援船出发![]() 小时后,失事船所在位置的横坐标为
小时后,失事船所在位置的横坐标为![]() .
.
(1)当![]() 时,写出失事船所在位置
时,写出失事船所在位置![]() 的纵坐标.若此时两船恰好会合,求
的纵坐标.若此时两船恰好会合,求
救援船速度的大小和方向;
(2)问救援船的时速至少是多少海里才能追上失事船?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com