已知函数f(x)=x3+3bx2+cx+bc-2b3(b,c∈R),函数g(x)=m[f(x)]2+p(其中m.p∈R,且mp<0),给出下列结论:
①函数f(x)不可能是定义域上的单调函数;
②函数f(x)的图象关于点(-b,0)对称;
③函数g(x)=可能不存在零点(注:使关于x的方程g(x)=0的实数x叫做函数g(x)的零点);
④关于x的方程g(x)=0的解集不可能为{-1,1,4,5}.
其中正确结论的序号为________(写出所有正确结论的序号).
②④
分析:①求导函数可得:f′(x)=3x
2+6bx+c,当36b
2-12c≤0时,f′(x)≥0,函数为增函数;
②验证f(-x-2b)=-f(x)即可;
③函数g(x)=m[f(x)]
2+p,∴g(x)=0时,[f(x)]
2=-
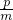
,此方程一定有解;
④关于x的方程g(x)=0的解集,即f(x)=0的解集,根据函数f(x)的图象关于点(-b,0)对称,可得结论
解答:①求导函数可得:f′(x)=3x
2+6bx+c,当36b
2-12c≤0时,f′(x)≥0,函数为增函数,故①不正确;
②f(-x-2b)=(-x-2b)
3+3b(-x-2b)
2+c(-x-2b)+bc-2b
3=-x
3-3bx
2-cx-bc+2b
3=-f(x),∴函数f(x)的图象关于点(-b,0)对称;
③函数g(x)=m[f(x)]
2+p,∴g(x)=0时,[f(x)]
2=-
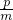
,此方程一定有解,∴函数g(x)=0存在零点,故③不正确;
④关于x的方程g(x)=0的解集,即f(x)=0的解集,根据函数f(x)的图象关于点(-b,0)对称,可得解集不可能为{-1,1,4,5},故④正确
故答案为:②④
点评:本题考查命题的真假判断,考查函数的性质,考查学生分析解决问题的能力,属于中档题.

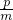 ,此方程一定有解;
,此方程一定有解;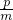 ,此方程一定有解,∴函数g(x)=0存在零点,故③不正确;
,此方程一定有解,∴函数g(x)=0存在零点,故③不正确;

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<