
【题目】若向量 ![]() =
= ![]() ,
, ![]() =(sinωx,0),其中ω>0,记函数f(x)=(
=(sinωx,0),其中ω>0,记函数f(x)=( ![]() +
+ ![]() )
) ![]() ﹣
﹣ ![]() .若函数f(x)的图象与直线y=m(m为常数)相切,并且切点的横坐标依次成公差是π的等差数列.
.若函数f(x)的图象与直线y=m(m为常数)相切,并且切点的横坐标依次成公差是π的等差数列.
(Ⅰ)求f(x)的表达式及m的值;
(Ⅱ)将f(x)的图象向左平移 ![]() 个单位,再将得到的图象上各点的纵坐标变为原来的2倍(横坐标不变)后得到y=g(x)的图象,求y=g(x)在
个单位,再将得到的图象上各点的纵坐标变为原来的2倍(横坐标不变)后得到y=g(x)的图象,求y=g(x)在 ![]() 上的值域.
上的值域.
【答案】解:(Ⅰ)∵向量 ![]() =
= ![]() ,
, ![]() =(sinωx,0),∴函数f(x)=(
=(sinωx,0),∴函数f(x)=( ![]() +
+ ![]() )
) ![]() ﹣
﹣ ![]() =
= ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() +sin2ωx﹣
+sin2ωx﹣ ![]() =
= ![]() sin2ωx﹣
sin2ωx﹣ ![]() cos2ωx=sin(2ωx
cos2ωx=sin(2ωx ![]() ),
),
∵函数f(x)的图象与直线y=m(m为常数)相切时,
切点的横坐标依次成公差是π的等差数列.
故T=π,m=±1,
即2ω=2,ω=1,
∴ ![]() ,m=±1
,m=±1
(Ⅱ)将f(x)的图象向左平移 ![]() 个单位,
个单位,
可得 ![]() 的图象,
的图象,
再将得到的图象上各点的纵坐标变为原来的2倍(横坐标不变)后得到y=g(x)= ![]() 的图象,
的图象,
当x∈ ![]() 时,
时, ![]() ∈
∈ ![]() ,
,
故当 ![]() =
= ![]() 即x=
即x= ![]() 时,函数最最大值2,
时,函数最最大值2,
当 ![]() =
= ![]() 即x=
即x= ![]() 时,函数最最小值﹣1,
时,函数最最小值﹣1,
故y=g(x)在 ![]() 上的值域为:[﹣1,2]
上的值域为:[﹣1,2]
【解析】(Ⅰ)由已知结合向量的数量积运算,倍角公式,和差角公式,可得f(x)的表达式及m的值;(Ⅱ)求出y=g(x)解析式,结合正弦函数的图象和性质,可得y=g(x)在 ![]() 上的值域.
上的值域.
【考点精析】认真审题,首先需要了解函数y=Asin(ωx+φ)的图象变换(图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象).
的图象).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知直线x﹣2y+2与圆C:x2+y2﹣4y+m=0相交,截得的弦长为 ![]()
(1)求圆C的方程;
(2)过点M(﹣1,0)作圆C的切线,求切线的直线方程;
(3)若抛物线y=x2上任意三个不同的点P、Q、R,且满足直线PQ和PR都与圆C相切,判断直线QR与圆C的位置关系,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点M(﹣1,0),N(1,0),曲线E上任意一点到M的距离均是到点N距离的 ![]() 倍.
倍.
(1)求曲线E的方程;
(2)已知m≠0,设直线l1:x﹣my﹣1=0交曲线E于A,C两点,直线l2:mx+y﹣m=0交曲线E于B,D两点,C,D两点均在x轴下方,求四边形ABCD面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,已知点
轴的正半轴为极轴建立极坐标系,已知点![]() 的直角坐标为
的直角坐标为![]() ,若直线
,若直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)求直线l和曲线![]() 的普通方程;
的普通方程;
(2)设直线l和曲线![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等边![]() 的边长为3,点
的边长为3,点![]() 分别为
分别为![]() 上的点,且满足
上的点,且满足![]() (如图1),将
(如图1),将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使二面角
的位置,使二面角![]() 成直二面角,连接
成直二面角,连接![]() ,
, ![]() (如图2)
(如图2)


(1)求证: ![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an+2﹣2an+1+an=0(n∈N*),a2=4,其前7项和为42,设数列{bn}是等比数列,数列{bn}的前n项和为Sn满足b1=a1﹣1,S30﹣(310+1)S20+310S10=0.
(1)求数列{an},{bn}的通项公式;
(2)令cn=1+log3 ![]() ,dn=
,dn= ![]() +
+ ![]() ,求证:数列{dn}的前n项和Tn≥
,求证:数列{dn}的前n项和Tn≥ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的左、右焦点分别为F1,F2,且离心率为
(a>b>0)的左、右焦点分别为F1,F2,且离心率为![]() ,M为椭圆上任意一点,当∠F1MF2=90°时,△F1MF2的面积为1.
,M为椭圆上任意一点,当∠F1MF2=90°时,△F1MF2的面积为1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知点A是椭圆C上异于椭圆顶点的一点,延长直线AF1,AF2分别与椭圆交于点B,D,设直线BD的斜率为k1,直线OA的斜率为k2,求证:k1·k2等于定值.
【答案】(Ⅰ)![]() (Ⅱ)见解析
(Ⅱ)见解析
【解析】
(Ⅰ)由题意可求得![]() ,则
,则![]() ,椭圆
,椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)设![]() ,
,![]() ,
,
当直线![]() 的斜率不存在或直线
的斜率不存在或直线![]() 的斜率不存在时,
的斜率不存在时,![]() .
.
当直线![]() 、
、![]() 的斜率存在时,
的斜率存在时,![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,联立直线方程与椭圆方程,结合韦达定理计算可得直线
,联立直线方程与椭圆方程,结合韦达定理计算可得直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,则
,则![]() .综上可得:直线
.综上可得:直线![]() 与
与![]() 的斜率之积为定值
的斜率之积为定值![]() .
.
(Ⅰ)设![]() 由题
由题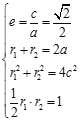 ,
,
解得![]() ,则
,则![]() ,
,![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)设![]() ,
,![]() ,当直线
,当直线![]() 的斜率不存在时,
的斜率不存在时,
设![]() ,则
,则![]() ,直线
,直线![]() 的方程为
的方程为![]() 代入
代入![]() ,
,
可得![]()
![]() ,
,![]() ,则
,则![]() ,
,
![]() 直线
直线![]() 的斜率为
的斜率为 ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,
![]() ,
,
当直线![]() 的斜率不存在时,同理可得
的斜率不存在时,同理可得![]() .
.
当直线![]() 、
、![]() 的斜率存在时,
的斜率存在时,![]() 设直线
设直线![]() 的方程为
的方程为![]() ,
,
则由 消去
消去![]() 可得:
可得:![]() ,
,
又![]() ,则
,则![]() ,代入上述方程可得:
,代入上述方程可得:
![]() ,
,![]() ,
,
则![]()
![]() ,
,
设直线![]() 的方程为
的方程为![]() ,同理可得
,同理可得![]() ,
,
![]() 直线
直线![]() 的斜率为
的斜率为
![]() 直线
直线![]() 的斜率为
的斜率为![]() ,
,![]()
 .
.
所以,直线![]() 与
与![]() 的斜率之积为定值
的斜率之积为定值![]() ,即
,即![]() .
.
【点睛】
(1)解答直线与椭圆的题目时,时常把两个曲线的方程联立,消去x(或y)建立一元二次方程,然后借助根与系数的关系,并结合题设条件建立有关参变量的等量关系.
(2)涉及到直线方程的设法时,务必考虑全面,不要忽略直线斜率为0或不存在等特殊情形.
【题型】解答题
【结束】
21
【题目】已知函数f(x)=(x+b)(![]() -a),(b>0),在(-1,f(-1))处的切线方程为(e-1)x+ey+e-1=0.
-a),(b>0),在(-1,f(-1))处的切线方程为(e-1)x+ey+e-1=0.
(Ⅰ)求a,b;
(Ⅱ)若方程f(x)=m有两个实数根x1,x2,且x1<x2,证明:x2-x1≤1+![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com