
【题目】已知三棱锥P-ABC的平面展开图中,四边形ABCD为边长等于![]() 的正方形,△ABE和△BCF均为正三角形,在三棱锥P-ABC中:
的正方形,△ABE和△BCF均为正三角形,在三棱锥P-ABC中:

(1)证明:平面PAC⊥平面ABC;
(2)若点M为棱PA上一点且![]() ,求二面角P-BC-M的余弦值.
,求二面角P-BC-M的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)如图①,设AC的中点为O,连结![]() .
.

由题意,得![]() ,PO=2,
,PO=2,![]() .
.
因为在△PAC中,PA=PC,O为AC的中点,所以PO⊥AC.
又因为在△POB中,PO=2,OB=2,PB=![]() ,
,![]() ,所以PO⊥OB.
,所以PO⊥OB.
因为AC∩OB=O,AC,OB平面ABC,所以PO⊥平面ABC.
又因为PO平面PAC,所以平面PAC⊥平面ABC.
(2)由PO⊥平面ABC,OB⊥AC,所以![]() .
.
于是以OC、OB、OP所在直线分别为x轴、y轴、z轴建立如图②所示的空间直角坐标系,
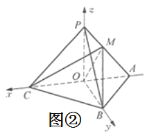
则![]() ,
,![]() ,
,
![]() ,
,![]() .
.
设平面MBC的法向量为![]() ,则由
,则由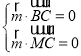 得
得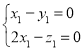 ,
,
令![]() ,则
,则![]() ,即
,即![]() .
.
设平面PBC的法向量为![]() ,由
,由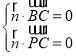 得
得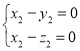 ,
,
令x2=1,则![]() ,即
,即![]() .
.
![]() .
.
由图可知,二面角P-BC-M的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】双十一购物狂欢节,是指每年11月11日的网络促销日,源于淘宝商城(天猫)2009年11月11日举办的网络促销活动,已成为中国电子商务行业的年度盛事.某生产商为了了解其生产的产品在不同电商平台的销售情况,统计了![]() 两个电商平台各十个网络销售店铺的销售数据:
两个电商平台各十个网络销售店铺的销售数据:
| 64 | 71 | 81 | 70 | 79 | 69 | 82 | 73 | 75 | 60 |
| 60 | 80 | 97 | 77 | 96 | 87 | 76 | 83 | 94 | 96 |
(1)作出![]() 两个电商平台销售数据的茎叶图,根据茎叶图判断哪个电商平台的销售更好,并说明理由;
两个电商平台销售数据的茎叶图,根据茎叶图判断哪个电商平台的销售更好,并说明理由;
(2)填写下面关于店铺个数的![]() 列联表,并根据列联表判断是否有
列联表,并根据列联表判断是否有![]() 的把握认为销售量与电商平台有关;
的把握认为销售量与电商平台有关;
销售量 | 销售量 | 总计 | |
| |||
| |||
总计 |
(3)生产商要从这20个网络销售店铺销售量前五名的店铺中,随机抽取三个店铺进行销售返利,则其中恰好有两个店铺的销售量在95以上的概率是多少?
附: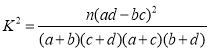 ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
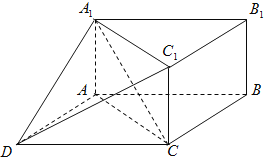
【题目】如图,三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() .以
.以![]() ,
,![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,连接
,连接![]() 和
和![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)若二面角![]() 为45°,
为45°,
①证明:平面![]() 平面
平面![]() ;
;
②求直线![]() 与平面
与平面![]() 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,平面
中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 是等腰直角三角形,且
是等腰直角三角形,且![]() ,
,![]() 平面
平面![]() ,
,![]() .
.

(1)求异面直线![]() 和
和![]() 所成角的余弦值;
所成角的余弦值;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为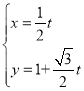 (t为参数),以直角坐标系
(t为参数),以直角坐标系![]() 的
的![]() 点为极点,
点为极点,![]() 为极轴,且长度单位相同,建立极坐标系,得曲线
为极轴,且长度单位相同,建立极坐标系,得曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的倾斜角;
的倾斜角;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司培训员工某项技能,培训有如下两种方式:
方式一:周一到周五每天培训1小时,周日测试
方式二:周六一天培训4小时,周日测试
公司有多个班组,每个班组60人,现任选两组![]() 记为甲组、乙组
记为甲组、乙组![]() 先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
第一周 | 第二周 | 第三周 | 第四周 | |
甲组 | 20 | 25 | 10 | 5 |
乙组 | 8 | 16 | 20 | 16 |
![]() 用方式一与方式二进行培训,分别估计员工受训的平均时间
用方式一与方式二进行培训,分别估计员工受训的平均时间![]() 精确到
精确到![]() ,并据此判断哪种培训方式效率更高?
,并据此判断哪种培训方式效率更高?
![]() 在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,过
,过![]() 的直线
的直线![]() 与抛物线C交于
与抛物线C交于![]() 两点,点A在第一象限,抛物线C在
两点,点A在第一象限,抛物线C在![]() 两点处的切线相互垂直.
两点处的切线相互垂直.
(1)求抛物线C的标准方程;
(2)若点P为抛物线C上异于![]() 的点,直线
的点,直线![]() 均不与
均不与![]() 轴平行,且直线AP和BP交抛物线C的准线分别于
轴平行,且直线AP和BP交抛物线C的准线分别于![]() 两点,
两点,![]() .
.
(i)求直线![]() 的斜率;
的斜率;
(ⅱ)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小芳、小明两人各拿两颗质地均匀的骰子做游戏,规则如下:若掷出的点数之和为4的倍数,则由原投掷人继续投掷;若掷出的点数之和不是4的倍数,则由对方接着投掷.
(1)规定第1次从小明开始.
(ⅰ)求前4次投掷中小明恰好投掷2次的概率;
(ⅱ)设游戏的前4次中,小芳投掷的次数为![]() ,求随机变量
,求随机变量![]() 的分布列与期望.
的分布列与期望.
(2)若第1次从小芳开始,求第![]() 次由小芳投掷的概率
次由小芳投掷的概率![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]()
![]() 这三个条件中任选一个,补充在下面问题中,并给出解答.
这三个条件中任选一个,补充在下面问题中,并给出解答.
设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,________,
,________,![]() ,若对于任意
,若对于任意![]() 都有
都有![]() ,且
,且![]() (
(![]() 为常数),求正整数
为常数),求正整数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com