
已知 的展开式的二项式系数的和比(3x-1)n的展开式的二项式系数和大992,求(2x-
的展开式的二项式系数的和比(3x-1)n的展开式的二项式系数和大992,求(2x-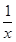 )2n的展开式中,(1)二项式系数最大的项;(2)系数的绝对值最大的项.
)2n的展开式中,(1)二项式系数最大的项;(2)系数的绝对值最大的项.
(1) T6=-8 064; (2) T4=-15 360x4.
解析试题分析:(1)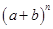 的二项式系数和为
的二项式系数和为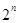 ,则由题可得
,则由题可得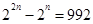 ,得
,得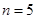 ,由二项式系数的性质知第
,由二项式系数的性质知第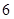 项最大;(2) 设第r+1项的系数的绝对值最大,可得到关于
项最大;(2) 设第r+1项的系数的绝对值最大,可得到关于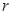 的不等式,解得
的不等式,解得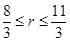 取整可知
取整可知 ,代回可得系数的绝对值最在的项为第
,代回可得系数的绝对值最在的项为第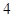 项.
项.
解:由题意知,22n-2n=992,
即(2n-32)(2n+31)=0,∴2n=32,解得n=5. 4分
(1)由二项式系数的性质知,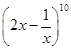 的展开式中第6项的二项式系数最大,即
的展开式中第6项的二项式系数最大,即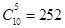 .
.
∴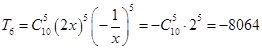 . 6分
. 6分
(2)设第r+1项的系数的绝对值最大,
∴ .
.
∴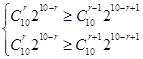 , 8分
, 8分
得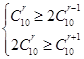 ,即
,即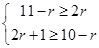 ,
,
解得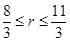 , 10分
, 10分
∵r∈Z,∴r=3.故系数的绝对值最大的是第4项,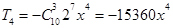 . 12分
. 12分
考点:二项式系数和项的系数.


科目:高中数学 来源: 题型:解答题
规定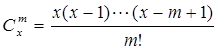 ,其中
,其中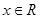 ,
, 是正整数,且
是正整数,且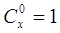 ,这是组合数
,这是组合数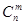 (
( 、
、 是正整数,且
是正整数,且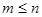 )的一种推广.如当
)的一种推广.如当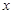 =-5时,
=-5时,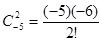
(1)求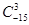 的值;
的值;
(2)设x>0,当x为何值时,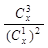 取得最小值?
取得最小值?
(3)组合数的两个性质;
①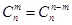 . ②
. ② .
.
是否都能推广到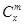 (
(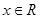 ,
, 是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有3名男生,4名女生,在下列不同要求下,求不同的排列方法总数:
(1)选其中5人排成一排;
(2)排成前后两排,前排3人,后排4人;
(3)全体排成一排,甲不站在排头也不站在排尾;
(4)全体排成一排,女生必须站在一起;
(5)全体排成一排,男生互不相邻;
(6)全体排成一排,甲、乙两人中间恰好有3人.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知非空有限实数集S的所有非空子集依次记为S1,S2,S3, ,集合Sk中所有元素的平均
值记为bk.将所有bk组成数组T:b1,b2,b3, ,数组T中所有数的平均值记为m(T).
(1)若S={1,2},求m(T);
(2)若S={a1,a2, ,an}(n∈N*,n≥2),求m(T).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设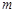 是给定的正整数,有序数组(
是给定的正整数,有序数组(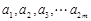 )中
)中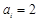 或
或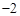
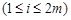 .
.
(1)求满足“对任意的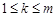 ,
,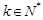 ,都有
,都有 ”的有序数组(
”的有序数组(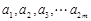 )的个数
)的个数 ;
;
(2)若对任意的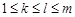 ,
,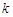 ,
, ,都有
,都有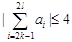 成立,求满足“存在
成立,求满足“存在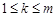 ,使得
,使得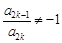 ”的有序数组(
”的有序数组(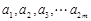 )的个数
)的个数 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com