
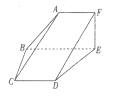
【题目】已知空间四边形![]() ,
, ![]() 分别在
分别在![]() 上,
上,
(1) 若![]() ,异面直线
,异面直线![]() 与
与![]() 所成的角的大小为
所成的角的大小为![]() ,求
,求![]() 和
和![]() 所成的角的大小;
所成的角的大小;
(2)当四边形![]() 是平面四边形时,试判断
是平面四边形时,试判断![]() 与
与![]() 三条直线的位置关系,并选择其中一种位置关系说明理由;
三条直线的位置关系,并选择其中一种位置关系说明理由;
(3)已知当![]() ,异面直线
,异面直线![]() 所成角为
所成角为![]() ,当四边形
,当四边形![]() 是平行四边形时,试判断
是平行四边形时,试判断![]() 点在什么位置时,四边形
点在什么位置时,四边形![]() 的面积最大,试求出最大面积并说明理由。
的面积最大,试求出最大面积并说明理由。
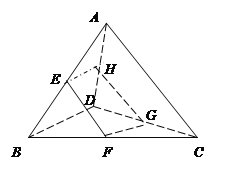
【答案】(1)![]() 或
或![]() (2)
(2)![]() 或者
或者![]() 相交,(3)
相交,(3)![]() 分别为
分别为![]() 中点时,四边形
中点时,四边形![]() 的面积最大,
的面积最大, ![]()
【解析】试题分析:(1)根据题意可得四边形![]() 为菱形,而菱形对角线平分对角可得
为菱形,而菱形对角线平分对角可得![]() 和
和![]() 所成的角大小(2)先定位置:
所成的角大小(2)先定位置: ![]() 或者
或者![]() 相交,再分情况证明:当
相交,再分情况证明:当![]() 时,利用线面平行性质与判定定理可得
时,利用线面平行性质与判定定理可得 ![]() ;当
;当![]() 相交时,可得
相交时,可得![]() 相交(3)先根据线线角得四边形
相交(3)先根据线线角得四边形![]() 一内角为
一内角为![]() ,利用平行四边形面积公式可得
,利用平行四边形面积公式可得![]() ,再根据相似比得
,再根据相似比得![]() ,最后根据基本不等式求最值
,最后根据基本不等式求最值
试题解析:解:(1)![]() 或
或![]()
(2)![]() 共面
共面![]() 或者
或者![]() 相交,设交点为
相交,设交点为![]()
(以下理由只要求写出一种即对)
![]() 时
时
![]() 且
且![]()
又![]() 且
且![]()
![]()
即三条直线互相平行
![]() 时
时
![]()
![]()
又![]()
![]()
又![]()
![]() 即三条直线交于一点
即三条直线交于一点
(3) ![]()
在![]() 中,
中, ![]() ,在
,在![]() 中,
中, ![]()
![]()
![]()
![]() 时
时![]() 取得最大值,即
取得最大值,即![]() 分别为
分别为![]() 中点时,四边形
中点时,四边形![]() 的面积最大,
的面积最大, ![]()


科目:高中数学 来源: 题型:
【题目】数列{an}中,an=32,sn=63,
(1)若数列{an}为公差为11的等差数列,求a1;
(2)若数列{an}为以a1=1为首项的等比数列,求数列{am2}的前m项和sm′ .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
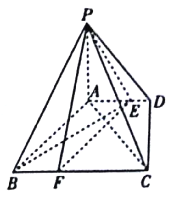
(Ⅰ)已知点![]() 在
在![]() 上,且
上,且![]() ,求证:平面
,求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)当二面角![]() 的余弦值为多少时,直线
的余弦值为多少时,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知E、F分别在正方体ABCD﹣A1B1C1D1的棱BB1、CC1上,且B1E=2EB,CF=2FC1 , 则面AEF与面ABC所成的二面角的正切值等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】鹰潭市龙虎山花语世界位于中国第八处世界自然遗产,世界地质公元、国家自然文化双遗产地、国家![]() 级旅游景区——龙虎山主景区排衙峰下,是一座独具现代园艺风格的花卉公园,园内汇集了3000余种花卉苗木,一年四季姹紫嫣红花香四溢.花园景观融合法、英、意、美、日、中六大经典园林风格,景观设计唯美新颖.玫瑰花园、香草花溪、台地花海、植物迷宫、儿童乐园等景点错落有致,交相呼应又自成一体,是世界园艺景观的大展示.该景区自2015年春建成试运行以来,每天游人如织,郁金香、向日葵、虞美人等赏花旺季日入园人数最高达万人.
级旅游景区——龙虎山主景区排衙峰下,是一座独具现代园艺风格的花卉公园,园内汇集了3000余种花卉苗木,一年四季姹紫嫣红花香四溢.花园景观融合法、英、意、美、日、中六大经典园林风格,景观设计唯美新颖.玫瑰花园、香草花溪、台地花海、植物迷宫、儿童乐园等景点错落有致,交相呼应又自成一体,是世界园艺景观的大展示.该景区自2015年春建成试运行以来,每天游人如织,郁金香、向日葵、虞美人等赏花旺季日入园人数最高达万人.
某学校社团为了解进园旅客的具体情形以及采集旅客对园区的建议,特别在2017年4月1日赏花旺季对进园游客进行取样调查,从当日12000名游客中抽取100人进行统计分析,结果如下:(表一)
年龄 | 频数 | 频率 | 男 | 女 |
| 10 | 0.1 | 5 | 5 |
[10,20) | ① | ② | ③ | ④ |
[20,30) | 25 | 0.25 | 12 | 13 |
[30,40) | 20 | 0.2 | 10 | 10 |
[40,50) | 10 | 0.1 | 6 | 4 |
[50,60) | 10 | 0.1 | 3 | 7 |
[60,70) | 5 | 0.05 | 1 | 4 |
[70,80) | 3 | 0.03 | 1 | 2 |
[80,90) | 2 | 0.02 | 0 | 2 |
合计 | 100 | 1.00 | 45 | 55 |
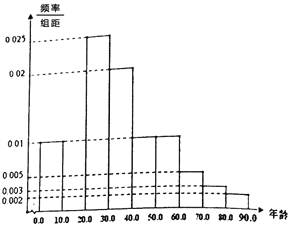
(1)完成表格一中的空位①-④,并在答题卡中补全频率分布直方图,并估计2017年4月1日当日接待游客中30岁以下人数.
(2)完成表格二,并问你能否有97.5%的把握认为在观花游客中“年龄达到50岁以上”与“性别”相关?
(3)按分层抽样(分50岁以上与50以下两层)抽取被调查的100位游客中的10人作为幸运游客免费领取龙虎山内部景区门票,再从这10人中选取2人接受电视台采访,设这2人中年龄在50岁以上(含)的人数为![]() ,求
,求![]() 的分布列
的分布列
(表二)
50岁以上 | 50岁以下 | 合计 | |
男生 | |||
女生 | |||
合计 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: 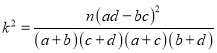 ,其中
,其中![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形, ![]() ,四边形
,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对应的边分别为a,b,c,且(2a﹣c)cosB=bcosC. (Ⅰ)求角B的大小;
(Ⅱ)若 ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面![]() 平面
平面![]() 四边形
四边形![]() 为直角梯形,
为直角梯形, ![]() 四边形
四边形![]() 为等腰梯形,
为等腰梯形, ![]() 且
且![]()
(Ⅰ)若梯形![]() 内有一点
内有一点![]() ,使得
,使得![]() 平面
平面![]() ,求点
,求点![]() 的轨迹;
的轨迹;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com