【答案】
分析:(1)设P1(x,y),根据题设的条件建立关于点P
1的坐标x,y的等式.
(2)设过P
1(x
1,y
1),P
2(x
2,y
2) 两点的直线P
1P
2的方程为:y=k(x-1)代入y
2=4x得到关于x的一元二次方程,利用根系关系得到x的一元二次方程,利用根系关系得到两根之和与两根之差.解出两线段长度的倒数和,解得其值为定值.
解答:解:(1)设P
1(x,y),则由:
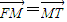
得M是线段FT的中点,得M(0,

)
∴
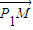
=(-x,

-y)
又∵
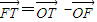
=(-2,t),
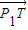
=(-1-x,t-y)
∵
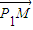
⊥
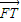
∴2x+t(

-y)=0 ①
∵
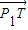 ∥
∥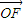
∴(-1-x)•0+(t-y)•1=0化简得:t=y ②
由①、②得:y
2=4x
这里用了参数方程的思想求轨迹方程;②也可以利用向量的几何意义,利用抛物线的定义判断轨迹为抛物线,从而求解.)
(2)易知F(1,0)是抛物线y
2=4x的焦点,由
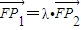
,
得(x
1,y
1),P
2(x
2设过P
1(x
1,y
1),P
2(x
2,y
2) 两点的直线P
1P
2的方程为:y=k(x-1)代入y
2=4x
得k
2x
2-2(k
2+2)x+k
2=0
则x
1x
2=1,x
1+x
2=
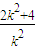
∴
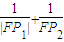 =
=
=
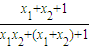
=1.
点评:考查用参数法求轨迹方程与直线与圆的位置关系,本题两个题运算量都较大,解题过程较长,要严谨做题.

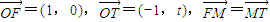 ,
,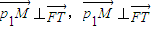 ,
,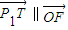 .
.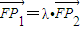 ,求证:
,求证: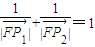 .
.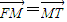 得M是线段FT的中点,得M(0,
得M是线段FT的中点,得M(0, )
)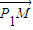 =(-x,
=(-x, -y)
-y)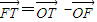 =(-2,t),
=(-2,t),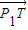 =(-1-x,t-y)
=(-1-x,t-y)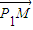 ⊥
⊥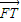 ∴2x+t(
∴2x+t( -y)=0 ①
-y)=0 ①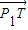 ∥
∥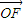
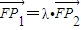 ,
,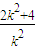
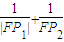 =
= =
=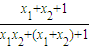 =1.
=1.
