
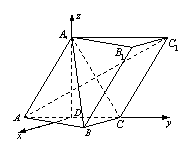
(08年鹰潭市一模理)(12分)已知斜三棱柱![]() ,
,![]() ,
,![]() ,
,![]() 在底面
在底面![]() 上的射影恰为
上的射影恰为![]() 的中点
的中点![]() ,又知
,又知![]() .
.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求![]() 到平面
到平面![]() 的距离;
的距离;
(Ⅲ)求二面角![]() 的大小.
的大小.

解析:解法![]() :(Ⅰ)∵
:(Ⅰ)∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() , 得
, 得![]() ,又
,又![]() ,
,
∴![]() 平面
平面![]() .…………………4分
.…………………4分
(Ⅱ)∵![]() ,四边形
,四边形![]() 为菱形,故
为菱形,故![]() ,
,
又![]() 为
为![]() 中点,知∴
中点,知∴![]() .取
.取![]() 中点
中点![]() ,则
,则
![]() 平面
平面![]() ,从而面
,从而面![]() 面
面![]() ,…………6分
,…………6分
过![]() 作
作![]() 于
于![]() ,则
,则![]() 面
面![]() ,在
,在![]() 中,
中,![]() ,故
,故![]() ,即
,即![]() 到平面
到平面![]() 的距离为
的距离为![]() .…………………8分
.…………………8分
(Ⅲ)过![]() 作
作![]() 于
于![]() ,连
,连![]() ,则
,则![]() ,从而
,从而![]() 为二面角
为二面角![]() 的平面角,在
的平面角,在![]() 中,
中,![]() ,∴
,∴![]() ,…………10分
,…………10分
在![]() 中,
中,![]() ,故二面角
,故二面角![]() 的大小为
的大小为![]() .
.
…………………12分
解法![]() :(Ⅰ)如图,取
:(Ⅰ)如图,取![]() 的中点
的中点![]() ,则
,则![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
又![]() 平面
平面![]() ,以
,以![]() 为
为![]() 轴建立空间坐标系, …………1分
轴建立空间坐标系, …………1分
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,由
,由![]() ,知
,知![]() ,
,
又![]() ,从而
,从而![]() 平面
平面![]() .…………………4分
.…………………4分
(Ⅱ)由![]() ,得
,得![]() .设平面
.设平面![]() 的法向量
的法向量
为![]() ,
,![]() ,
,![]() ,
,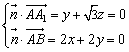 ,
,
设![]() ,则
,则![]() .…………6分
.…………6分
∴点![]() 到平面
到平面![]() 的距离
的距离![]() .…………………8分
.…………………8分
(Ⅲ)设面![]() 的法向量为
的法向量为![]() ,
,![]() ,
,![]() ,
,
∴ .…………10分
.…………10分
设![]() ,则
,则![]() ,故
,故![]() ,根据法向量的方向
,根据法向量的方向
可知二面角![]() 的大小为
的大小为![]() .…………………12分
.…………………12分



科目:高中数学 来源: 题型:
(08年鹰潭市一模理)(14分)已知函数![]() 满足
满足![]() ,
,![]() ,
,![]() ;且使
;且使![]() 成立的实数
成立的实数![]() 只有一个。
只有一个。
(Ⅰ)求函数![]() 的表达式;
的表达式;
(Ⅱ)若数列![]() 满足
满足![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,证明数列
,证明数列![]() 是等比数列,并求出
是等比数列,并求出![]() 的通项公式;
的通项公式;
(Ⅲ)在(Ⅱ)的条件下,如果![]() ,
,
![]() ,证明:
,证明:![]() ,
,![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年鹰潭市一模理) (12分)在一次语文测试中,有一道我国四大文学名著《水浒传》、《三国演义》、《西游记》、《红楼梦》与它们的作者的连线题,已知连对一个得2分,连错一个不得分.
(Ⅰ)求该同学得分的分布列;
(Ⅱ)求该同学得分的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年鹰潭市一模理) 已知![]() 为第二象限角,且
为第二象限角,且![]() ,那么
,那么![]() 的取值范围是( )
的取值范围是( )
A. ( -1 ,0 ) B. ( 1 , ![]() ) C. ( -1 ,1 ) D. ( -
) C. ( -1 ,1 ) D. ( -![]() ,-1 )
,-1 )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com